Lesson 1: Atomic Mass and Atom Counting

Part d: Gram-Mole-Atoms Relationship

Part a: Atomic Mass
Part b: Measuring Atomic Mass
Part c: The Mole
Part d: Grams-Moles-Atoms Relationship

 

The Goals:

Lesson 1d will focus on the use of conversion factors to …

• Determine the number of moles that are equal to a given number of atoms of an element.
• Determine the number of atoms that are equal to a given number of moles of an element.
• Determine the number of moles that are equal to a given mass in grams of an element.
• Determine the mass in grams that are equal to a given number of moles of an element.
• Determine the number of atoms that are equal to a given mass in grams of an element.
• Determine the mass in grams that are equal to a given number of atoms of an element.

 
 
 

The Factor Label Method Returns

The factor label method was introduced in Lesson 4 of Chapter 1. The factor label method involves the use of conversion factors to convert from a given quantity in one set of units to the same or a different quantity in a different set of units. A conversion factor is a multiplying fraction with a number and a unit in both the numerator and the denominator. The six stated goals above can be solved using the factor label method.
 
Successful use of the factor label method requires the ability to create conversion factors from an equivalence statement. An equivalence statement equates two numerical values having different units. Conversion factors are easily made from equivalence statements by placing one side of the equation in the numerator and the other side in the denominator. Units must be present in the conversion factor. As shown below, two conversion factors can be made from every equivalence statement.  
The above conversion factors relate the number of atoms to a mole (abbreviated mol). Each will be used to accomplish the stated goals of Lesson 1d.
 
A second commonly used conversion factor relates the mass in grams of an element to the number of moles of atoms of that same element. This conversion factor is based upon the molar mass concept. As discussed in Lesson 1c, the molar mass of an element is the grams per 1 mole of atoms of that element. Molar mass values are found in the individual cells of the periodic table. For helium, the molar mass is 4.00 grams per 1 mole of helium. As shown below, two conversion factors can be made from this statement.
   
The above conversion factors relate the mass in grams to a mole of that element. Each will commonly be used to accomplish the stated goals of Lesson 1d.
 
Conversion factors are used to convert between quantities. The basic idea is to use a conversion factor with a denominator unit that matches the unit of the given quantity. That unit will cancel and the unit of the numerator is the unit on the answer. A complete discussion with numerous examples can be found in Lesson 4a of Chapter 1 of this Chemistry Tutorial.
 
     

Atoms ⇔ Moles

The two conversion factors below are used to convert atoms to moles and moles to atoms.
   
Conversion Factor #1 is used to convert from atoms to moles. The denominator has units of atoms. When this fraction is used as a multiplier, it will cancel the atoms of the given quantity. The unit on the result is the uncancelled mol in the numerator.  
 
Conversion Factor #2 is used to convert from moles to atoms. The denominator has units of mol (mole). When the fraction is used as a multiplier, it will cancel the moles of the given quantity. The unit on the result is the uncancelled atoms of the numerator.  
 
Example #1
A sample of sulfur contains 5.15x10²² atoms. Determine the number of moles of sulfur in the sample?
 
Solution:
The given quantity is the number of atoms - 5.15x10²² atoms. The target unit is the moles of sulfur. Conversion Factor #1 will be used since it has atoms in the denominator. Using the factor with atoms in the denominator will cancel the atoms of the given quantity. The mol will not cancel and that will be the unit on the answer. Begin by writing down the given quantity with its unit. Then set up the conversion factor with units and numbers. Cancel (cross out) the atoms of the given quantity and in the denominator of the conversion factor. Now it’s time to multiply the given value by the numerator value and to divide by the denominator value.
   
The answer is 0.0855 mol. It has been rounded to the third significant digit.
 
 
Example #2
A lab procedure requires the use of 2.50 moles of copper. How many atoms of copper would this be?
 
Solution:
The given quantity is the number of moles – 2.50 mol. The target unit is the number of atoms. Conversion Factor #2 will be used since it has mol in the denominator. Using the factor with mol in the denominator will cancel the mol of the given quantity. The atoms will not cancel and that will be the unit on the answer. Begin by writing down the given quantity with its unit. Then set up the conversion factor with units and numbers. Cancel (cross out) the mol of the given quantity and in the denominator of the conversion factor. Finally, multiply the given value by the numerator value and divide by the denominator value.
   
The answer is 1.51x10²⁴ atoms. It has been rounded to the third significant digit.
 
   
 

Moles ⇔ Grams

The two conversion factors below are used to convert from moles to grams and from grams to moles.
   
The value X in these factors depends on what the element E is. The element E will be stated in the problem. Locate the element E on the periodic table and use the listed molar mass as the X value.
 
Conversion Factor #3 is used to convert from moles to grams. The denominator has units of mol. When the fraction is used as a multiplier, it will cancel the mol of the given quantity. The unit on the result is the g (grams) of the numerator.  
 
Conversion Factor #4 is used to convert from grams to moles. The denominator has units of g (grams). When the fraction is used as a multiplier, it will cancel the g of the given quantity. The unit on the result is the mol (moles) from the numerator.  
 
 
Example #3
The science department just purchased a 4.58 mol sample of sodium. (They’re planning on having some fun.) How many grams of sodium are in the sample?
 
Solution:
The given quantity is the moles – 4.58 mol of Na. The target unit is the grams of Na. Conversion Factor #3 will be used since it has mol in the denominator. Using this factor with mol in the denominator will cancel the mol of the given quantity. The g will not cancel and that will be the unit on the answer. Begin by writing down the given quantity with its unit. Then set up the conversion factor with units and numbers. Cancel (cross out) the mol of the given quantity and in the denominator of the conversion factor. Now it’s time to multiply the given value by the numerator value and to divide by the denominator value.
   
The answer is 105 g. It has been rounded to the third significant digit.
 
 
Example #4
Millie Meeder has a chemistry problem in which she must convert 68.5 g of aluminum to moles of aluminum. Show Millie how it’s done.
 
Solution:
The given quantity is the mass of aluminum – 68.5 g Al. The target unit is the moles of Al. Conversion Factor #4 will be used since it has g in the denominator. Using the factor with g in the denominator will cancel the g of the given quantity. The mol Al will not cancel and that will be the unit on the answer. Begin by writing down the given quantity with its unit. Then set up the conversion factor with units and numbers. Cancel (cross out) the g Al of the given quantity and in the denominator of the conversion factor. Finally, multiply the given value by the numerator value and divide by the denominator value.
   
The answer is 2.54 mol Al. It has been rounded to the third significant digit.
 
   
 
 

Atoms ⇔ Grams

So far, we have seen examples in which just a single conversion factor is used to convert the unit of the given quantity to the target unit. Now we will see instances in which two conversion factors are required.
 
These two-step problems of converting from atoms to grams or from grams to atoms can be thought of as a combining of the types of problems we have already solved. For instance, the conversion of the given quantity atoms to the mass in grams can be done by first converting from atoms to moles and then from moles to grams. These two steps can be done together by stringing together the two conversion factors in consecutive fashion.
   
The process of converting from a given quantity of grams to the number of atoms can be done in two steps as well. First convert from grams to moles and then from moles to atoms.
   
Both Avogadro’s number (Conversion Factors #1 and #2) and molar mass (Conversion Factors #3 and #4) will be used to do these conversions.
   
 
Example #5
What is the mass (in grams) of 2.29 x10²¹ atoms of neon?
 
Solution:
The given quantity is the atoms – 2.29 x10²¹ atoms of Ne. The target unit is the grams of Ne. Conversion Factor #1 will be used to convert the unit on the given quantity (atoms) to moles. Then Conversion Factor #3 will be used to convert the moles to the target unit grams. The two conversion factors will be strung together in consecutive fashion. Units will be cancelled (crossed out).
 
To facilitate the idea of unit conversions, we first show the set-up of conversion factors without any numbers. Observe the cancellation of units.
   
Once we have the conversion factors set up to perform the proper cancellation of units, we insert the numbers in the appropriate locations. We carefully solve on our calculator by multiplying the given value (2.29 x10²¹) by the two numerator values and then dividing by the two denominator values.
   
The answer is 0.767 g. It has been rounded to the third significant digit.
 
 
Example #6
How many atoms are in 3.12-gram copper (pure) penny?
 
Solution:
The given quantity is the mass – 3.12 g Cu. The target unit is the atoms of Cu. Conversion Factor #4 will be used to convert the unit on the given quantity (g Cu) to moles. Then Conversion Factor #2 will be used to convert the moles to the target unit - atoms of Cu. The two conversion factors will be strung together in consecutive fashion. Units will be cancelled (crossed out).
 
The conversion factor set up is first done without any numbers. Observe the cancellation of units.
   
Once we have the conversion factors set up to perform the proper cancellation of units, we insert the numbers in the appropriate locations. We carefully solve on our calculator by multiplying the given value (3.12) by the two numerator values and then dividing by the two denominator values.
   
The answer is 2.96x10²² atoms. It has been rounded to the third significant digit.
 
 
 
 

The Mass of an Atom

The following problem can be a stumper. However, it helps to understand the problem as being no different than Example 5. Review Example 5 (above) if needed, then return to observe the problem and solution.
 
Example #7
Determine the mass in grams of a zinc atom.
 
Solution:
This problem is just like Example 5 in that the given quantity is the number of atoms and the target quantity is the mass in grams. The actual number of atoms (1) is a bit subtle since it wasn’t explicitly listed in the problem statement. The given quantity is the number of atoms – 1 atom of Zn. The target unit is the grams of Zn. Conversion Factor #1 will be used to convert the unit on the given quantity (atoms) to moles. Then Conversion Factor #3 will be used to convert the moles to the target unit grams. The two conversion factors will be strung together in consecutive fashion. Units will be cancelled (crossed out). Once the conversion factors are set up to perform the proper cancellation of units, we insert the numbers in the appropriate locations. We carefully solve on our calculator by multiplying the given value (1) by the two numerator values and then dividing by the two denominator values.
   
Not surprisingly, the mass of one atom in grams is really small. The answer is 1.09x10^-22 g. It has been rounded to the third significant digit.
 
 
 
 

Giving Professor HONClBrIF Some Attention

In Chapter 2 of this Chemistry Tutorial, we mentioned seven elements that when found in nature by themselves exist as diatomic molecules as opposed to isolated atoms.
   
These are elements that exist as molecules and not atoms. Because there are two atoms per molecule, the molar mass of these molecules is twice the average atomic mass (for a single atom) that is stated on the periodic table. Special attention will have to be given to the wording of the problem in order to determine if the problem pertains to the diatomic form (as found naturally in nature) or the monatomic form. Example #8 below is a problem where the diatomic form must be considered.

 
Example #8
Kal Chapotato breathes in approximately 0.70 moles of oxygen every hour. What mass of oxygen is Kal consuming?
 
Solution:
The given quantity is the moles of oxygen. Since Kal is breathing this from the air, it can be assumed to exist as diatomic oxygen – O₂.  So, the given quantity is 0.70 mol O₂. The target unit is the grams of O₂. Conversion Factor #3 will be used since it has mol in the denominator. Using this factor with mol in the denominator will cancel the mol of the given quantity. The g will not cancel and that will be the unit on the answer. Note that the molar mass of diatomic oxygen (twice the 15.9994 value listed on the table) is used since oxygen is one of the seven elements that exist naturally in diatomic form. Begin by writing down the given quantity with its unit. Then set up the conversion factor with units and numbers. Cancel (cross out) the mol of the given quantity and in the denominator of the conversion factor. Now it’s time to multiply the given value by the numerator value and to divide by the denominator value.
   
The answer is 22 g. It has been rounded to the second significant digit since the given value has only two significant digits.
 
 
 
 

Counting the Number of Atoms

Lesson 1 began with the question of how do chemists (and chemistry students) count the number of atoms in a sample of matter. And now we know. We first use a mass balance to determine the mass of the sample in grams. Then we use a couple of conversion factors that include molar mass values and Avogadro’s number to determine the number of atoms. The calculation looks just like Example 6 above.
 
Be proud of yourself! You are now equipped with another superpower. You can count the number of atoms in a sample of matter. A very small percentage of the people on this planet can do that!
   
 
 

Before You Leave

• Download our Study Card on Mole Conversions. Save it to a safe location and use it as a review tool. (Coming Soon.)
• Our Calculator Pad section has two sets of Practice Problems on this topic. Your answers are evaluated and feedback is provided; you have infinite opportunities to correct your mistakes. Try …
  • Problem Set PMG5 – Avogadro’s Number.
  • Problem Set PMG6 – Particles-Moles-Grams 1.
• The Check Your Understanding section below includes questions with answers and explanations. It provides a great chance to self-assess your understanding.

 
 
 

Check Your Understanding

Use the following questions to assess your understanding. Tap the Check Answer buttons when ready.
 
1. Identify the following statements as being proper or improper equivalence statements.

1. 6.022 x 10²³ atoms Sulfur = 1.000 mol Sulfur 
   
   Check Answer
   Answer: Proper
   
   There is an Avogadro's number of atoms in a mole of atoms. 
   
    
   
    
2. 32.07 g Sulfur = 1.000 mol Sulfur 
   
   Check Answer
   Answer: Proper
   
   The mass in grams of a mole of atoms is equal to the average atomic mass for that element as listed on the periodic table. It lists 32.07-ish for sulfur.
   
    
   
    
3. 6.022 x 10²³ grams Iron = 1.000 mol Iron 
   
   Check Answer
   Answer: Improper
   
   Avogadro's number relates the number of atoms (NOT the mass in grams) to a mole. The molar mass value of iron should show up on the left side of this equation.
   
    
   
    
4. 6.022 x 10²³ atoms Boron = 10.81 grams Boron 
   
   Check Answer
   Answer: Proper (Sort of)
   
   The number of atoms are related to the mole and the mole is related to the mass in grams for that specific element. This is set up correctly but not in the manner in which we would recommend. Particularly for beginners to factor label method (and to most teachers who should be far from beginners), it is wise to use two conversion factors here. Each comes from two different equivalence statements. Do be careful about taking shortcuts with the factor label method. It is often a shorter distance to a wrong answer than it is to a right answer.
   
    

 
 
2. Each conversion factor shown below is successfully used to solve for an unknown in the problem. For each, indicate what the given quantity and the target quantity are. That is, what is G (with unit) and what is T (with unit)?

 
 
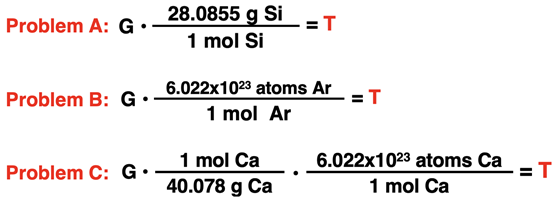
3. Aaron Agin is having troubles with his factor label method. Consider his three failed conversions below. Identify what went wrong with his conversion factor set up.

 


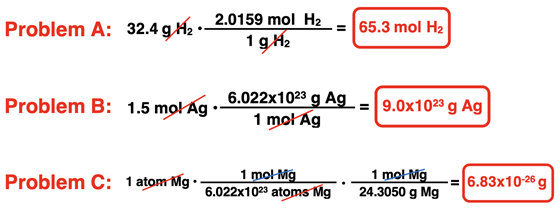
For more practice use the links to the Calculator Pad as provided in the Before You Leave section above.