Lesson 4: Calculations in Chemistry

Part a: The Factor Label Method

Part 4a: The Factor Label Method
Part 4b: Unit Conversions
Part 4c: Significant Digits Revisited

 

Mathematics in Chemistry

Chemistry is a quantitative science. Numbers are included. You will collect numerical data. You will graph numerical data. You will calculate other quantities from this numerical data. You will learn formulas for calculating quantities like the amount of a substance, the amount that reacts, the pressure, the volume, the reaction rate, the concentration, and much more. Because Chemistry is a quantitative science, there is no escaping the use of numerical information. And that means that mathematics will be a common tool used by a Chemistry student.
  
Often times, the mathematics is as simple as using a formula, substituting numbers, and solving for the quantities. On other occasions, you will have to algebraically rearrange an equation before doing the substituting and solving. But the most frequently used calculations will be reliant upon a method that comes by many names. We will refer to it as the factor label method.
 
 
 

The Factor Label Method

The factor label method involves the use of converting factors to convert from a given quantity in one set of units to the same or a different quantity in a different set of units. A converting factor (more commonly called a conversion factor) is a multiplying factor that has a numerator and a denominator – a fraction with an upstairs (numerator) and a downstairs (denominator). Both the upstairs and the downstairs will include a number and a unit. As you will find, the unit is essential. In fact, the factor label method is all about units.
 
Here's a simple example: suppose you’re told that the length of a pencil is 8.4 cm and you wish to determine its length in inches. You are told that 1 inch = 2.54 cm. You can solve this with the use of a conversion factor.

 

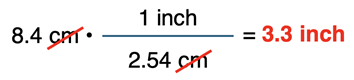
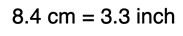
From the above work, we can conclude that the amount 8.4 cm is equal to 3.3 inches.
 
In the above example, the cm unit on the given quantity (8.4 cm) is cancelled by the cm unit in the denominator of the conversion factor. The unit that is not cancelled is the unit on the answer. In the above example, the unit inch was not cancelled and that is the unit on the answer. The numerical part of the answer is found by taking the given number (8.4) and multiplying by the numerator(s) and dividing by the denominator(s).
 

  
Let’s step it up a bit with a related example. Determine the length of the 8.4 cm pencil in feet (ft) if given 1 inch = 2.54 cm and 12 inch = 1 ft. This will require the use of two conversion factors. The start of a solution is shown below. The two conversion factors are set up (without numbers). The goal of the factor label method is to cancel units and to acquire the desired unit for the answer. The downstairs unit of the first factor should match the given unit. The downstairs unit of the second factor should match the upstairs unit of the first factor.

 

Conversion factors are used to cancel units. Avoid memorizing! Instead learn the skill of unit cancellation. Most of that skill is associated with setting up the units as shown above. If you can form the conversion factors with the units in the correct location, then adding numbers will be easy. In the statement 1 inch = 2.54 cm, the 2.54 is with cm and the 1 is with inch. So put the 2.54 number in the denominator with cm and put the 1 in the numerator with inch. That’s easy. Using the same logic for 12 inch = 1 ft, put 12 in the denominator of the second conversion factor with inch and 1 in the numerator with ft. The full solution is shown below.
 

 

 

Equivalence Statements and Conversion Factors

The 1 inch = 2.54 cm is what we call an equivalence statement. It relates the two sets of units to one another. Every equivalence statement can be turned into two different conversion factors that allow you to convert between the two quantities. They differ by which unit is on the top and which is on the bottom. For instance, 1 inch = 2.54 cm can be made into these two conversion factors:

 

 
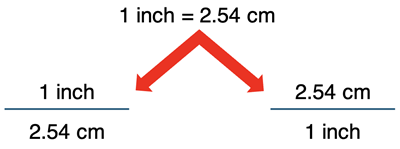
You will only use one of these two conversion factors in a problem. The one that you use depends on which unit you wish to cancel. The unit in the denominator should match the unit on the given quantity in order to cancel units.
 
Equivalence statements are not the only information by which conversion factors are made. Conversion factors can be created from verbal statements as well. If it is stated that a solid has a density of 8.29 g/mL, then you can make the following conversion factors from it:

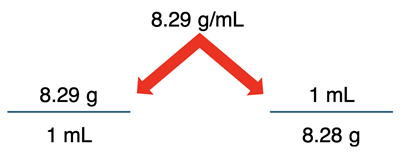
When you see a compound unit like g/mL or m/s, you can interpret it to mean “g per 1 mL” or “m per 1 s”. So, when you write the conversion factor you will insert a “1” with the milliliter (mL) or with the second (s).
 

 

 
The Method of the Factor Label Method

Use the following step-by-step method to approach conversion factor problems.

1. Identify the given quantity with its unit.
2. Identify the target unit.
3. Identify relevant equivalence statements; these must include units.
4. Write down the given quantity with its unit and set up a conversion factor next to it.
5. Enter the denominator unit in order to cancel the given unit. Then enter the numerator unit. Use an equivalence statement to do this.
6. Enter numerical values into the numerator and denominator.
7. Is the numerator unit the target unit? If not, then set up a new conversion factor and repeat steps 5 and 6. If it is the target unit, then calculate your answer by multiplying the given amount by all the numerator numbers and dividing by all the denominator numbers. Record your result with the unit.

 

 
 

The Anatomy of a Conversion Factor Solution

Suppose that you are asked to convert 5.0 miles to centimeters (cm). You are given:

• 1 mi = 5280 ft
• 12 in = 1 ft
• 2.54 cm = 1 in

 
The arrangement of conversion factors is shown below.
 

 
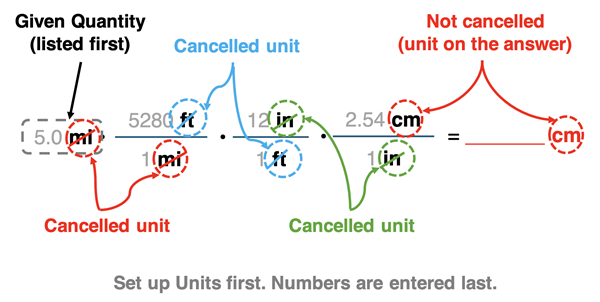
The graphic is presented as an example of how to structure your conversion factors. The starting point is always the given quantity (5.0 mi). The units are arranged with cancellation in mind. A unit in the numerator (or on the given quantity) is cancelled when the identical unit is located in the denominator of another conversion factor. The numbers always come last. Use the equivalence statement(s) to decide where the numbers are located. For example, 5280 is put in the numerator with ft and 1 in the denominator with mi because in the equivalence statement, 5280 is with ft and 1 is with mi (5280 ft = 1 mi).
 

 

More Examples

Make an effort to solve the following example problems using the factor label method. Tap the Check Answer button when ready to view the solution.

Example 1:
In a rather impulsive moment, Johnny went to the store and bought 6.6 puggets.  There are 24 callies in 1 pugget and 16.4 illies in 1 callie.  How many illies did Johnny buy?
 

 
 

Example 2:
In the country of Figglethorpe, a student can receive 1 A for earning a total of 89 picklades.  Given that 1 picklade = 14.2 nappiewaters and 1 nappiewater = 24.5 papliweeds, how many papliweeds are needed to get an A?
 



Note that in both cases, the final answer has been rounded to two significant digits. We will have more to say about rounding and significant digits later in Lesson 4.
 
 

 

Why It Works

You might be wondering, what kind of mathematical sorcery is this? I’ve never had a course in math that covered the factor label method; are making this stuff up? It might surprise you that the factor label method is built on very simple mathematical principles that you already know. These include:

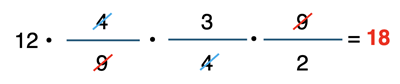
• When there are a series of multiplying factors, identical numbers found in the numerator and denominator will cancel each other. The example below shows the 4s and the 9s cancelling each other.
  
  
  The same principle applies to units.

 

• The value of any fraction is equal to the numerator divided by the denominator. If the numerator is equal to the denominator, then the value must be 1.
  
  
  
  Since conversion factors are made from equivalence statements, the numerator is equal to the denominator and the value is 1. While the numerator and denominator units are different, the amount in the numerator is equal to the amount in the denominator. In the above example 1 inch = 2.54 cm.

 

• Multiplying any amount by 1 does not change the amount.
  
  
  
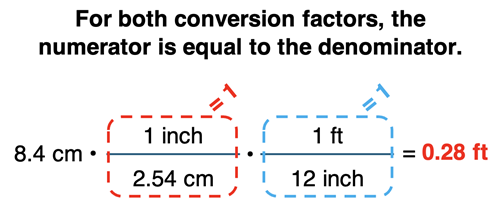
  Conversion factors are a means of multiplying a given amount by factors that are equal to 1. The number in the numerator and the denominator are different only because the accompanying unit is different. The result is that you end up with a different unit when you are done but the amount of that quantity is equal to the given amount expressed in a different unit. You have simply converted the unit.

 
As you can see, the factor label method is not mathematical sorcery at all. It is basic mathematics.
 
 

Answering Your “Yes. But …” with a “Yes. But …”

It is not unusual for a student to say at this point in the course “I can do this without conversion factors.” The fact is the student might be correct. Every problem on this page can be reasoned through without a conversion factor. But as problems become more difficult (and they will become more difficult), the likelihood of a student being successful without using conversion factors decreases. And the difficulty of solving problems without conversion factors increases. Meanwhile, the difficulty of solving problems with conversion factors decreases as you gain more and more practice. The method of solving problems with conversion factors never changes regardless of the topic. This is a skill you can use the entire course. And for some teachers, it is not even optional (and we don’t blame them for saying so). The moral of the story is to invest in learning how to use conversion factors early and the return on your investment will be much appreciated.
 
 
 

Before You Leave

• Download our Study Card on the Factor Label Method. Save it to a safe location and use it as a review tool. 
• The Check Your Understanding section below include questions and problems with answers, explanations, and solutions. It provides a great chance to self-assess your understanding.

 
   

Check Your Understanding

Use the following questions to assess your understanding. Tap the Check Answer buttons when ready.
 
1. Write two conversion factors from the equivalence statement 1 mile = 5280 ft.

 

2. For the given information in each of the following statements, write two conversion factors.
a. There are 100 cm in 1 meter.
b. The car was traveling 22.6 m/s
c. The moon makes a complete orbit around the Earth every 27.3 days.
d. One mole of atoms is equivalent to 6.022 x 10²³ atoms





 
3. Solve the following problems using the factor label method:
 
Mr. H is playing a card game called "Nonsense" with his buddies.  In one of his luckier hands, he is dealt 4 willets.  Three willets are equivalent to 50 points.  Every 16 points is equivalent to 11.5 mummies.  How many mummies can Mr. H win with this particular hand?

 

 

If 67 floppies = 1 zip and 10 zips = 1 jazz and 27.9 jazz = 3.1 WWW, then use conversion factors to determine the number of floppies in 1 WWW.