Hold down the T key for 3 seconds to activate the audio accessibility mode, at which point you can click the K key to pause and resume audio. Useful for the Check Your Understanding and See Answers.
Lesson 1: Describing a Gas
Part b: Pressure-Volume-Temperature-Moles
Part a: The Nature of a Gas
Part b: Pressure-Volume-Temperature-Moles
The BIG 4 Gas Variables
A sample of gas is described by four variables – pressure (P), temperature (T), volume (V), and the number of moles (n). We will come to know these variables by their symbols P, T, V, and n. We will refer to these four quantities quite regularly throughout the unit. Beginning in Lesson 2, we will learn that a change in one of these variables will affect one or more of the other variables. The values of P, V, T, and n are dependent upon one another. Before we explore their interdependency, let’s ensure that we have a strong conceptual grasp of their meaning.
Pressure
Gases push. Gas particles are in constant random motion about its container, colliding with one another and with the container walls. With each collision with a container wall, a gas particle exerts a force on the wall. With a seemingly uncountable number of tiny particles, each undergoing several collisions per second, the amount of cumulative force on the wall surface can be quite astounding. This cumulative force is the cause of pressure.
The pressure of a gas refers to the intensity of its pushing power upon the surfaces of the container. Pressure is defined as the force (F) per unit area (A). The pressure of a gas sample is the cumulative amount of force resulting from particle-wall collisions divided by the total surface area of the wall. Given that gas particles are so small, you might think they would exert an undetectable amount of pressure under typical room conditions. But the gas in the room that you are in may be exerting as much as 15 pounds (67 N) of force on every square inch of the surface.
The atmosphere is a large sea of gases whose pressure cannot be ignored. At sea level, atmospheric pressure if 14.7 pounds per square inch (psi). As you sit, walk, sleep, and study, you can count on about 14.7 pounds of force on every square inch of your body.* Let’s translate that to a force upon the top of your head, assuming you’re a flat top. We will estimate the average flat top to have a surface area of 40 in2 (5 in x 8 in). With 14.7 pounds per each square inch, the total amount of force on the flat top of your head is 588 pounds (2620 N). That’s the equivalent of an oversized gorilla sitting on top of your head. Now that’s pressure! Gases really do push.
* Atmospheric pressure is altitude dependent. It is less at higher altitudes.
Gases push in all direction, not just downward. This is because pressure is the result of gas particles colliding upon surfaces. Gas particles fill the container and move in every direction. They can collide with the top of objects, with the sides of objects, and with the bottom of objects. As such, gases push in all directions.
Pressure Units
There are a variety of units that are used to express the pressure of a gas. In the previous discussion, we have been using pounds per square inch (lbs/in2 or psi). While the unit provides handy way to discuss pressure as a force per area ratio, it is not the most universal unit for pressure. A listing of commonly used pressure units is shown at the right. As you progress through the Chapter, you will need to gain some familiarity with these units and their abbreviations. And you will need to be able to convert between units. To do such conversions, you will need some equivalence statements to form conversion factors.
1.00 atm = 101325 Pa = 101325 N/m2 = 760 mm Hg = 760 torr = 14.7 psi
To illustrate the use of these unit equivalencies to convert between pressure units, consider the following example problem.
Example:
A pressure warning in a car indicates a tire has a gauge pressure of 29.5 psi. Convert this gauge pressure to atmosphere (atm) and to kiloPascal (kPa).
Solution:
As in all conversion problems, this problem is solved using the factor label method. A conversion factor is formed from the equivalence statement in order to cancel the given unit and convert to the desired unit. We always advise setting up the units first. After all, the problem is all about units. The set up for the conversion from the given unit of psi to atm is shown below. The unit psi is placed in the denominator of the conversion factor in order to cancel the give unit (psi).
Once the solution is set up with units, numbers are inserted into the conversion factor and the gauge pressure in atm is calculated.
The set up for the conversion from psi to kPa is shown below. Two conversion factors are used. The first factor converts from psi to Pa. The unit equivalency is given above. The second conversion factor is used to convert from Pascal to kiloPascal. In the metric system, the Greek prefix kilo- means 1000; so, 1 kPa is equivalent to 1000 Pa.
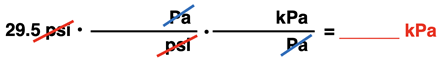
Once the conversion factors have been set up to cancel units and to acquire the desired unit, numbers are inserted into the conversion factors and the answer is calculated.
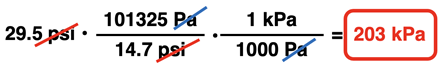
You might have noticed that we introduced a new term in this example problem - gauge pressure. Gauge pressure refers to the pressure of a sample of gas relative to the surrounding air pressure. It is a relative pressure as opposed to an absolute pressure. In this case, the gauge pressure inside the tire is 2.01 atm. This indicates that the pressure inside the tire is 2.01 atm greater than the pressure outside the tire. If the pressure outside the tire is 1.00 atm, then the absolute pressure is 3.01 atm.
Barometers and Manometers
Barometers and manometers are instruments that are used to measure pressure. A barometer is used to measure the pressure of a room or the atmosphere at a given location. A mercury barometer is shown at the right. It consists of a dish of liquid mercury. A tall tube (approximately 1-m high), open at one end, is filled with mercury. It is then inverted and its open end is submerged in a dish containing mercury. The mercury level in the tube drops slightly leaving a vacuum in the space above it. Because there is a no gas in the top of the tube, the liquid mercury adjusts its height until the weight of the mercury column equals the force with which the air in the room pushes down on the mercury in the dish. Thus, the height of the mercury column is proportional to the pressure in the room. This height is measured from the top of the mercury in the column to the top of the mercury in the dish. The measurement is usually made in units of millimeter and the room pressure is expressed with the unit mm Hg.
The first barometer was invented by Italian physicist Evangelista Torricelli in 1643. The pressure unit torr is named after him. A torr is equivalent to and used interchangeably with the unit mm Hg. The use of mercury in the barometer was for practical reasons. While not as abundant as water, mercury is one of the denser liquids known. With a density of 13.6 g/cm3, a mercury column will rise to a height of 760 mm at sea level. This means a mercury barometer can fit in a typical room. Under the same conditions, a water barometer would display water rising to a height of 10.3 meter (33.9 feet). Such a barometer will not fit in a typical room and a good-sized ladder would be required to read it.
Image: Public Domain
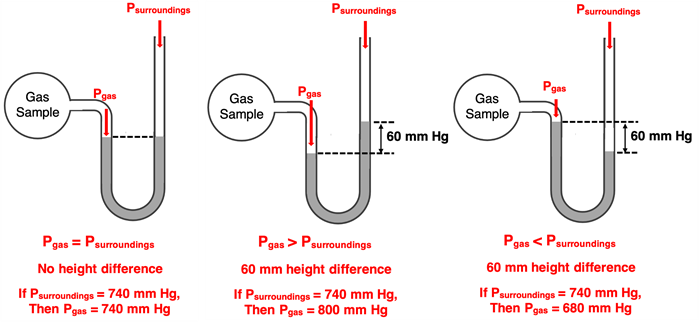
While a barometer is used to measure room pressure or atmospheric pressure, a manometer is used to measure the pressure of a sample of gas. A typical manometer consists of a vessel containing the gas; the vessel is attached to a U-shaped tube filled with mercury. The diagram at the right shows an open-end manometer. The right side of the U-tube is open to the surrounding atmosphere. The gas sample and the surroundings both push upon the mercury column. You can think of it as a push-of-war, similar to the more familiar tug-of-war.
If the gas sample and the surroundings push with the same pressure, then the mercury level will be at the same height on both sides of the U-tube. If the gas sample pushes on the mercury with a greater pressure than the surroundings, then the mercury will be higher on the surrounding’s side of the U-tube. And finally, if the surroundings have a greater pressure, then the mercury will rise higher on the sample’s side of the U-tube. By measuring the difference in mercury height of the two sides of the column, one can determine the gauge pressure. This gauge pressure is the relative pressure and indicates the difference in pressure between the gas sample and the surroundings. If the pressure of the surroundings are known, then the gauge pressure can be determined by subtraction or addition.
Kelvin Temperature
Temperature is one of those scientific quantities that is easier to explain than it is to define. If forced to define it, we’d resort to the ever-so-enlightening definition that temperature is what the thermometer reads. A classic (i.e., liquid) thermometer is a device that consists of a liquid-filled bulb that is connected to a very narrow column referred to as a capillary tube. Liquids expand with increasing temperature. So as the temperature increases, the distance that the liquid expands through the capillary tube increases. The thermometer is calibrated and marked with a scale that allows one to read the temperature in Celsius or Fahrenheit units. You have likely used such a thermometer in a science class. Liquid thermometers have been and are being replaced by digital thermometers that rely on more electronic methods of determining temperature.
While Celsius and Fahrenheit may be more popular, the Kelvin scale is the accepted metric scale for temperature measurements. The Kelvin scale was discussed in Chapter 1 of our Tutorial as part of our introduction to the metric system. A comparison of the three scales - Kelvin, Celsius, and Fahrenheit - is shown in the graphic below.
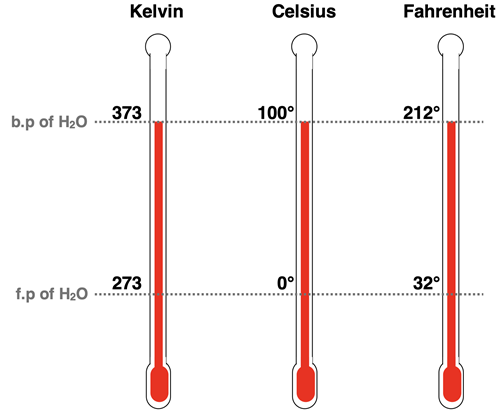
The following formulas can be used to convert between the various scales:
Kelvin Temperature = Celsius Temperature + 273.15
Celsius Temperature = Kelvin Temperature - 273.15
Fahrenheit Temperature = Celsius Temperature * 1.8 + 32
Celsius Temperature = (Fahrenheit Temperature – 32) ÷ 1.8
Thermometers are Speedometers
A thermometer is essentially a speedometer. Higher thermometer readings indicate that the gas particles are moving with a greater kinetic energy. Kinetic energy, the energy of motion, is a measure of the speed at which particles are moving. Lower thermometer readings indicate that the gas particles have less kinetic energy and are moving slower. A more sophisticated definition of temperature is to say that it is a measure of the amount of kinetic energy possessed by a sample of matter.
(Animation: Public Domain)
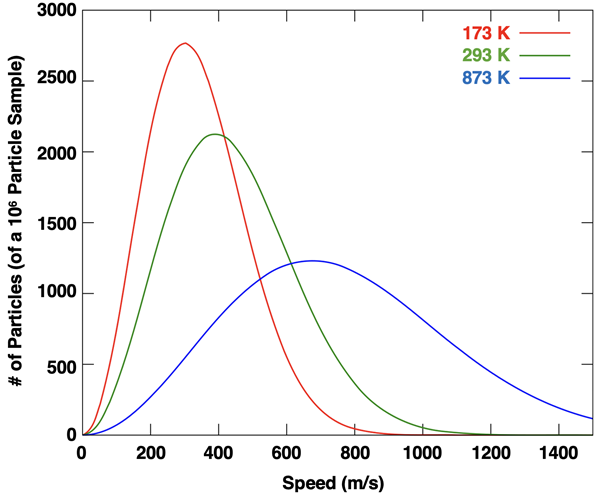
As mentioned earlier in Lesson 1, there is a range of speeds with which the gas particles are moving. Inspect the animation above and notice that some particles are traveling slow and others fast. It is the transfer of kinetic energy from a fast-moving particle to a slow-moving particle during a collision that leads to this range of speeds. Increasing temperatures cause the average kinetic energy to increase and expands the range of kinetic energy values. The graph below is known as a Maxwell-Boltzmann Distribution curve. Three different Kelvin temperatures are shown. As the Kelvin temperature is increased, the range of speeds increases. At higher temperatures, the most frequent speed is a faster speed. The temperature provides a measure of the average particle speed. And it is in this sense that a thermometer is a speedometer.
Volume
Volume refers to the amount of space occupied by an object. As we discussed earlier in Lesson 1, a gas fills the entire volume of the container. For this reason, the volume of a gas is dependent on and equal to the volume of the container. The standard metric unit of volume is the liter (abbreviated L). Because Chemistry labs typically deal with smaller sized samples of chemicals, we often express the volume in milliliter (abbreviated mL) or cubic centimeter (abbreviated cm3).
The volume of a gas sample can be determined in a couple of ways. The first set of measurement methods depend on an understanding of geometry. If the container is a rectangular prism (3-dimensional rectangle), then the volume can be determined by measuring the length, width, and height of the container. The volume is then calculated as the L•W•H.
Similarly, if the container is a cylinder or a sphere then specific measurements (radius, height, circumference, etc.) can be made and the geometry of the specific shape can be used to determine the volume.
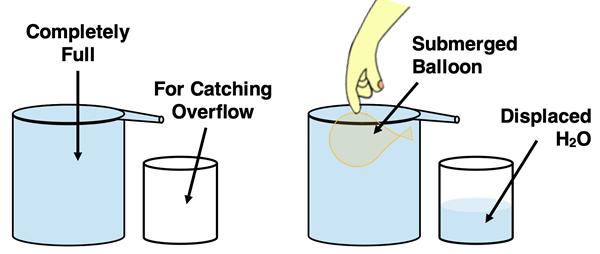
Other common methods of determining the volume of a gas container involve water displacement. Suppose you have a small balloon that is filled with gas and you wish to measure its volume. The balloon has an irregular shape so you are unable to use geometry to obtain an accurate measurement. So, you are left to measuring the volume by water displacement. Here’s the method: Fill a large container to the rim with water. Obtain an empty beaker and set it next to the container full of water. Completely submerge the balloon in the water. The balloon displaces the water and it overflows the container. Use the empty beaker to catch all the water that overflows. Then use a graduated cylinder to measure the volume of the water that overflows. This volume is equal to the volume of the balloon.
The Number of Moles
The final gas variable is the number of moles of gas in the sample. As we discussed in Chapter 7, the mole is the counting unit in Chemistry. One mole of a substance consists of 6.022x1023 particles of that substance. As we learned, the means of counting that many small particles involves determining the mass of the particles. Once the mass is determined, the molar mass of the gas can be used to determine the number of moles of gas particles.
As an example, suppose we use careful measurements to determine that the mass of oxygen (O2) gas in a large is 2.14 grams. The molar mass of oxygen is 32.0 g/mol. By dividing the mass by the molar mass, we can determine that there are 0.0669 moles of O2 particles in the container. In this example, we see how massing is a means of counting the number of gas particles in a sample of a known substance.
Next Up: Gas Laws
As we continue on to Lesson 2, we will put our understanding of pressure, volume, temperature, and the number of moles to use as we explore how a change in one these variables will affect the other variables associated with a gas.
Before You Leave
- Download our Study Card on Gas Variables. Save it to a safe location and use it as a review tool. (Coming Soon.)
- Try our Pressure Concepts Concept Builder. Activities 2 and 3 provide great practice with pressure units and manometer readings.
- Our Calculator Pad provides awesome practice solving chemistry math problems. Try Problem Set GL1 on Pressure and Temperature Conversions and Problem Set GL2 on Manometers and Barometers.
- The Check Your Understanding section below include questions with answers and explanations. It provides a great chance to self-assess your understanding.
Check Your Understanding
Use the following questions to assess your understanding. Tap the Check Answer buttons when ready.
1. What is the cause of pressure in a sample of gas?
2. For the following pairs of pressure values, identify the one that is a larger value.
- 1 atm vs. 1 psi
- 1 atm vs. 101 Pa
- 101 Pa vs. 101 kPa
- 760 mm Hg vs. 1 psi
3. Convert from 2.5 atm to mm Hg. Show your conversion factors.
4. Based on the diagram at the right, what is the pressure of the room.
5. For the three open-end barometers below, what is the pressure of the gas. The room pressure is 750 mm Hg.
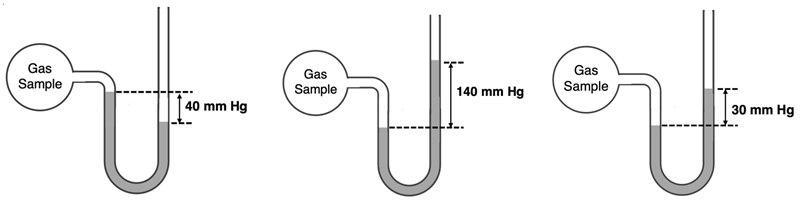
6. Explain why all the particles in a sample of gas are not moving with the same speed?
7. What affect does n increase in temperature have upon the speed of particles in a gas sample?
8. A sample of nitrogen gas (N2) is determined to have a mass of 7.0 grams. Determine the number of moles of N2 particles in the sample.