Hold down the T key for 3 seconds to activate the audio accessibility mode, at which point you can click the K key to pause and resume audio. Useful for the Check Your Understanding and See Answers.
Lesson 2: Gas Laws
Part a: Pressure and Temperature
Part a: Pressure and Temperature
Part b:
Volume and Temperature
Part c:
Pressure and Volume
Part d:
Volume and the Number of Moles
Part e:
The Ideal Gas Law
Part f:
Combined Gas Law
Part g:
Dalton's Law of Partial Pressure
Part h:
Graham's Law of Effusion
The Experiment
 Let’s begin our investigation of the gas laws by considering an experiment that is often performed in a Chemistry course. The experiment involves an air-filled flask that is equipped with a pressure sensor. The flask is sealed and rigid, preventing changes in the volume and the number of moles of gas. A thermometer is used to measure temperature. The flask is submerged in a beaker of chilled water. After adjusting to the temperature of the water, the pressure and temperature are measured. The process is repeated for several water samples of varying temperatures from just above 0°C up to 85°C. Sample data and the graph for such an experiment is shown below.
Let’s begin our investigation of the gas laws by considering an experiment that is often performed in a Chemistry course. The experiment involves an air-filled flask that is equipped with a pressure sensor. The flask is sealed and rigid, preventing changes in the volume and the number of moles of gas. A thermometer is used to measure temperature. The flask is submerged in a beaker of chilled water. After adjusting to the temperature of the water, the pressure and temperature are measured. The process is repeated for several water samples of varying temperatures from just above 0°C up to 85°C. Sample data and the graph for such an experiment is shown below.
(Image Source: Vernier Science Education)

A Deeper Look at the Data
The data and graph show a clear pattern for the relationship between pressure and temperature. The relationship is linear and begs the mathematician in us to write an equation in y = m•x + b form. But not so fast. Let’s take a deeper look.
Let’s take the line on the graph and extend it leftward until it intersects with the x-axis. At what temperature does the pressure drop to 0 atm? The result is shown below.
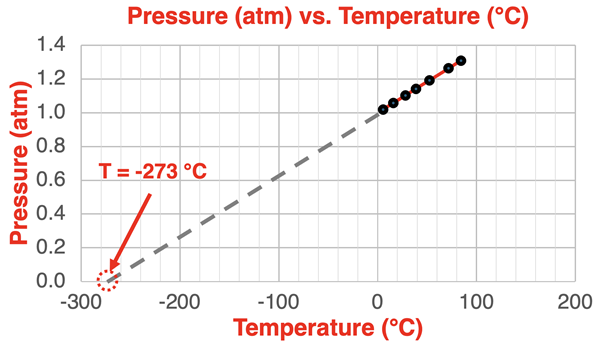
The temperature at which the pressure drops to 0 atm is approximately -273°C. Do you recognize that number? That is a temperature of 0 on the Kelvin temperature scale. That is generally referred to as absolute zero … the lowest temperature theoretically achievable. At this temperature, all particle motion ceases. At this temperature, particles will not collide with the container walls. There can be no pressure without such collisions. Particles are frozen in place and the pressure is 0.
There is one final adjustment that we will make to this graph. Let’s change the temperature scale to Kelvin and plot Pressure (atm) vs. Temperature (K).

Now we have a plot that is linear and has a y-intercept of 0. At this point we will give in to our inner mathematician and write an equation that fits the data. Using slope-intercept format (y = mx + b), we can assert that
Pressure (atm) = m • Temperature (K)
where m represents the slope of the line. In the case of this gas sample, the slope is 0.00366 atm/K. Experiments of this nature have been repeated numerous times and the results confirm the conclusion that the pressure of a gas is directly proportional to its Kelvin temperature.
The Gay-Lussac Gas Law
Our simple experiment leads us to the first of many gas laws that we will be discussing in Lesson 2. It is often referred to as the Gay-Lussac law, in honor of French chemist Joseph Gay-Lussac. (There is some dispute as to whether the law was discovered by Gay-Lussac or Guillaume Amontons.) The law can be stated as follows:
For a sample of gas with a constant volume and number of moles, the pressure of the gas is directly proportional its Kelvin temperature.
This proportionality statement is often written in equation form as
P = k•T
where P is the pressure, T is the Kelvin temperature, and k is a proportionality constant.
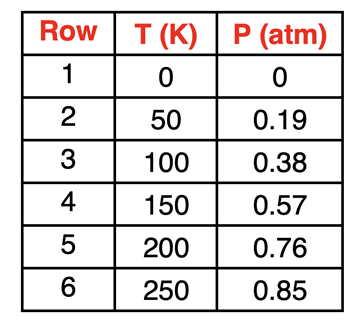
The idea of a directly proportional relationship indicates that the factor by which the Kelvin temperature is changed is the same factor by which the pressure changes. The sample data at the right illustrate this relationship. A doubling of the Kelvin temperature causes a doubling of the pressure. We see this pattern in Rows 2 and 3. The temperature is doubled from 50 K to 100 K and the pressure is doubled as a result, from 0.19 atm to 0.38 atm. Similarly, a tripling of the Kelvin temperature causes a tripling of the pressure. Once more, this is observed in Rows 2 and 4. The temperature is tripled from 50 K to 150 K and the pressure is tripled as a result, from 0.19 atm to 0.57 atm. Finally, a quadrupling of the Kelvin temperature causes a quadrupling of the pressure. We see this pattern in Rows 2 and 5. The temperature is quadrupled from 50 K to 200 K and the pressure is quadrupled from 0.19 atm to 0.76 atm.
The State Equation
As we have mentioned, a sample of gas is described by four variables - pressure, temperature, volume, and the number of moles. Gas samples often change the values of these variables. As we have seen on this page, the pressure and temperature change in direct proportion to one another. We might say that the gas sample changes from one state with a set of P-T-V-n conditions to another state with a different set of a set of P-T-V-n conditions. This is what we call a state change.
While the equation P = k•T communicates a useful proportionality, it is often more useful to express the relationship as a state equation. A state equation relates the variable values at one state to the variable values for another state after a change has occurred. The conversion of P = k•T to a state equation takes the following logical progression:
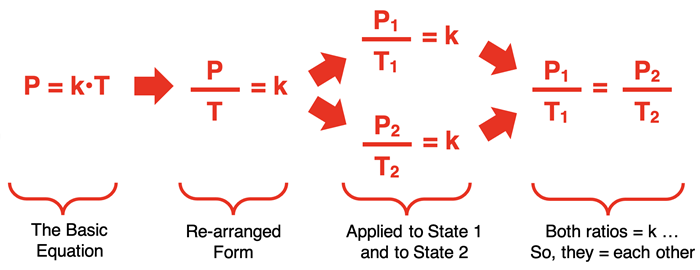
In the last step, a state equation is generated that relates the pressure and temperature in one state (P1 and T1) to the pressure and temperature of a second state (P2 and T2). This is one of the forms in which the Gay-Lussac law is commonly stated.

This state equation is often used in the solution of gas law problems. Here are two examples with accompanying solutions. Additional examples are provided in the Check Your Understanding section.
Example 1
Suppose a tennis ball contains 119 mL of gas and is pressurized to 32.0 psi at a temperature of 41.7°C. What is the internal pressure of the ball if the temperature drops to 4.2 °C? Assume a constant volume.
Solution
We recommend that you begin by writing down the given values, equating them with the appropriate symbol. Then identify the unknown value. Finally, substitute the numerical values into the equation and solve using proper algebra. The solution looks like this:
Given:
P1 = 32.0 psi
Temp1 = 41.7°C ... (add 273.15 for K) ==> T1 = 314.85 K
Temp2 = 4.2°C ... (add 273.15 for K) ==> T2 = 277.35 K
Unknown: P2 = ???
Equation: (P1 / T1) = (P2 / T2)
Rearrange equation to solve for P2: P2 = T2 • P1 / T1
Substitute values into the equation P2 = (277.35 K) • (32.0 psi) / (314.85 K)
Use your calculator to solve: P2 = 28.2 psi (rounded from 28.18866 …)
Note that the temperature values must be converted to Kelvin temperature before substituting into the equation. The pressure can be any pressure unit.
Example 2
The new helium gas cylinders have just arrived at the loading dock of a local party store. In the cool January air, the 20.0-L cylinders have a pressure of 68.6 atm. Once brought into the store, the cylinder’s temperatures increases to 27.1°C and the pressure adjusts to 76.1 atm. What is the outdoor temperature in °C?
Solution
We will use the same approach as before, organizing our given information, identifying the unknown, and substituting and solving with good algebra. We will once again be certain to use the equation with Kelvin temperature values.
Given:
P1 = 68.6 atm
P2 = 76.1 atm
Temp2 = 27.1°C ... (add 273.15 for K) ==> T2 = 300.25 K
Unknown: Temp1 = ???
Equation: (P1 / T1) = (P2 / T2)
Rearrange equation to solve for T1: T1 = T2 • P1 / P2 (requires a few algebra steps)
Substitute values into the equation: T1 = (300.25 K) • (68.6 atm) / (76.1 atm)
Use your calculator to solve: T1 = 270.65900 … K
Now convert to °C:
Temp1 = 270.65900 … K - 273.15 K
Temp1 = -2.5 °C (rounded from -2.4909986 …)
Conclusion
The pressure-temperature relationship is the first of several gas laws presented in Lesson 2. We will take a very similar approach with each law, beginning with sample data and analysis and progressing to the use of a state equation that can be used to solve problems. Next up is the Volume and Temperature. But before you move onward, please check out our learning suggestions below.
Before You Leave
- Download our Study Card on Pressure and Temperature. Save it to a safe location and use it as a review tool.
- Try our Pressure and Temperature Concept Builder. It coordinates well with this lesson and provides exceptional practice.
- Problem Set GL3 in our Calculator Pad section provides six awesome practice problems. Visit Pressure and Temperature.
- The Check Your Understanding section below include questions with answers and explanations. It provides a great chance to self-assess your understanding.
Check Your Understanding
Use the following questions to assess your understanding. Tap the
Check Answer buttons when ready.
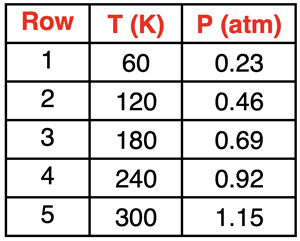
1. Consider the table at the right in answering the questions.
- Identify two sets of two rows that illustrate that a doubling of the temperature will double the pressure.
- Complete the sentence: Rows 1 and 5 illustrate that increasing the Kelvin temperature by a factor of ______ will cause the pressure to __________ (increase, decrease) by a factor of _____.
- Predict the value of the pressure when the Kelvin temperature is 360 K.
- Predict the value of the pressure when the Kelvin temperature is 480 K.
- Predict the value of the pressure when the Kelvin temperature is 150 K.
2. Which change would cause the temperature of a gas sample to increase?
- Increase the pressure of the gas.
- Decrease the pressure of the gas.
3. Starting with the state equation P
1/T
1 = P
2/T
2, use algebra to write it in four different algebraic forms. Generate a P
1 =, a P
2 =, a T
1 =, and a T
2 = equation.
4. A whip cream aerosol can has a volume of 350 mL and a pressure of 2.50 atm in the refrigerator at 5˚C. What pressure would be exerted on this can if it is thrown into a fire and heated to 650˚C? (
P.S. Don't do this at home ... or anywhere for that matter.)
5. The propane gas cannister attached to the gas grill reads a pressure of 68.2 psi on August 15 (a 96.5°C). It isn’t used for the rest of the summer and fall. What pressure will it have on January 15 when the temperature drops to 14.2°C?