Refraction and Lenses Review
Navigate to:
Review Session Home - Topic Listing
Refraction and Lenses - Home || Printable Version || Questions with Links
Answers to Questions: All || #1-#20 || #21-#34 || #35-#46
Part A: Multiple Choice
1. The best definition of refraction is ____.
|
a. passing through a boundary
|
b. bouncing off a boundary
|
|
c. changing speed at a boundary
|
d. changing direction when crossing a boundary
|
|
Answer: D
Bouncing off a boundary (choice b) is reflection. Refraction involves passing through a boundary (choice a) and changing speed (choice c); however, a light ray can exhibit both of these behaviors without undergoing refraction (for instance, if it approaches the boundary along the normal). Refraction of light must involve a change in direction; the path must be altered at the boundary.
|
2. If carbon tetrachloride has an index of refraction of 1.461, what is the speed of light through this liquid? (c = 3 x 108 m/s)
|
a. 4.38 x 108 m/s
|
b. 2.05 x 108 m/s
|
c. 4.461 x 108 m/s
|
d. 1.461 x 108 m/s
|
|
Answer: B
Use the equation v=c/n where n = 1.461 and c = speed of light in a vacuum (3x108 m/s).
|
[ #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #10 | #11 | #12 | #13 | #14 | #15 | #16 | #17 | #18 | #19 | #20 | #21 | #22 | #23 | #24 | #25 | #26 | #27 | #28 | #29 | #30 | #31 | #32 | #33 | #34 | #35 | #36 | #37 | #38 | #39 | #40 | #41 | #42 | #43 | #44 | #45 | #46 ]
3. A ray of light in air is incident on an air-to-glass boundary at an angle of 30. degrees with the normal. If the index of refraction of the glass is 1.65, what is the angle of the refracted ray within the glass with respect to the normal?
|
a. 56 degrees
|
b. 46 degrees
|
c. 30. degrees
|
d. 18 degrees
|
|
Answer: D
Use Snell's law:
ni * sine(Theta i) = nr * sine(Theta r)
where
ni =1.00 (in air), Theta i=30. degrees, nr =1.65
Substitute and solve for Theta r.
sine(Theta r) = 1.00 * sine(30. degrees) / 1.65 = 0.3030
Theta r = invsin(0.3030) = 17.6 degrees
|
[ #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #10 | #11 | #12 | #13 | #14 | #15 | #16 | #17 | #18 | #19 | #20 | #21 | #22 | #23 | #24 | #25 | #26 | #27 | #28 | #29 | #30 | #31 | #32 | #33 | #34 | #35 | #36 | #37 | #38 | #39 | #40 | #41 | #42 | #43 | #44 | #45 | #46 ]
4. If the critical angle for internal reflection inside a certain transparent material is found to be 48.0 degrees, what is the index of refraction of the material? (Air is outside the material).
|
a. 1.35
|
b. 1.48
|
c. 1.49
|
d. 0.743
|
|
Answer: A
The critical angle is the angle of incidence (which is always in the more dense material) for which the angle of refraction is 90 degrees.
Apply this to Snell's law equation:
nr * sine(48.0 deg) = 1.00 * sine (90.0 deg)
Solve for nr.
nr = 1.00/sin(48.0 deg) = 1.35
|
[ #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #10 | #11 | #12 | #13 | #14 | #15 | #16 | #17 | #18 | #19 | #20 | #21 | #22 | #23 | #24 | #25 | #26 | #27 | #28 | #29 | #30 | #31 | #32 | #33 | #34 | #35 | #36 | #37 | #38 | #39 | #40 | #41 | #42 | #43 | #44 | #45 | #46 ]
5. Carbon disulfide (n = 1.63) is poured into a container made of crown glass (n = 1.52). What is the critical angle for internal reflection of a ray in the liquid when it is incident on the liquid-to-glass surface?
|
a. 89.0 degrees
|
b. 68.8 degrees
|
c. 21.2 degrees
|
d. 4.0 degrees
|
|
Answer: B
The critical angle is the angle of incidence (which is always in the more dense material) for which the angle of refraction is 90 degrees.
Apply this to Snell's law equation:
1.63* sine(Theta critical.) = 1.52 * sine (90)
Solve for Theta critical.
sine(Theta critical.) = 1.52/1.63 = 0.9325
Theta critical. = invsine(0.9325) = 68.8 degrees
|
[ #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #10 | #11 | #12 | #13 | #14 | #15 | #16 | #17 | #18 | #19 | #20 | #21 | #22 | #23 | #24 | #25 | #26 | #27 | #28 | #29 | #30 | #31 | #32 | #33 | #34 | #35 | #36 | #37 | #38 | #39 | #40 | #41 | #42 | #43 | #44 | #45 | #46 ]
6. Carbon tetrachloride (n = 1.46) is poured into a container made of crown glass (n = 1.52). If the light ray in glass incident on the glass-to-liquid boundary makes an angle of 30 degrees with the normal, what is the angle of the corresponding refracted ray with respect to the normal?
|
a. 55.5 degrees
|
b. 29.4 degrees
|
c. 31.4 degrees
|
d. 19.2 degrees
|
|
Answer: C
Use Snell's law:
ni * sine(Theta i) = nr * sine(Theta r)
where
ni =1.52 (in glass), Theta i=30 degrees (angle in glass), nr =1.46 (in carbon tetrachloride)
Substitute and solve for Theta r
1.52 * sin(30 deg) = 1.46 * sin(Theta r)
[1.52 * sin(30 deg)]/1.46 = sin(Theta r)
0.5205 = sin(Theta r)
Theta r = invsine(0.5205) = 31.4 degrees
|
[ #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #10 | #11 | #12 | #13 | #14 | #15 | #16 | #17 | #18 | #19 | #20 | #21 | #22 | #23 | #24 | #25 | #26 | #27 | #28 | #29 | #30 | #31 | #32 | #33 | #34 | #35 | #36 | #37 | #38 | #39 | #40 | #41 | #42 | #43 | #44 | #45 | #46 ]
7. A light ray in air is incident on an air to glass boundary at an angle of 45.0 degrees and is refracted in the glass of 30.0 degrees with the normal. What is the index of refraction of the glass?
|
a. 2.13
|
b. 1.74
|
c. 1.23
|
d. 1.41
|
|
Answer: D
Use Snell's law:
ni * sine(Theta i) = nr * sine(Theta r)
where
ni=1.00 (in air), Theta i=45.0 degrees (angle in air), Theta r=30.0 degrees (in glass)
Substitute and solve for nr.
1.00 * sine(45.0 deg) = nr * sine(30.0 deg)
1.00 * sine(45.0 deg) / sine(30.0 deg) = nr
nr = 1.41
|
[ #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #10 | #11 | #12 | #13 | #14 | #15 | #16 | #17 | #18 | #19 | #20 | #21 | #22 | #23 | #24 | #25 | #26 | #27 | #28 | #29 | #30 | #31 | #32 | #33 | #34 | #35 | #36 | #37 | #38 | #39 | #40 | #41 | #42 | #43 | #44 | #45 | #46 ]
8. A beam of light in air is incident at an angle of 35 degrees to the surface of a rectangular block of clear plastic (n = 1.5). The light beam first passes through the block and reemerges from the opposite side into air at what angle to the normal to that surface?
|
a. 42 degrees
|
b. 23 degrees
|
c. 35 degrees
|
d. 59 degrees
|
|
Answer: C
The light ray bends towards the normal upon entering and away from the normal upon exiting. If the opposite sides are parallel to each other and surrounded by the same material, then the angle at which the light enters is equal to the angle at which the light exits.
|
[ #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #10 | #11 | #12 | #13 | #14 | #15 | #16 | #17 | #18 | #19 | #20 | #21 | #22 | #23 | #24 | #25 | #26 | #27 | #28 | #29 | #30 | #31 | #32 | #33 | #34 | #35 | #36 | #37 | #38 | #39 | #40 | #41 | #42 | #43 | #44 | #45 | #46 ]
9. A light ray in air enters and passes through a block of glass. What can be stated with regard to its speed after it emerges from the block?
|
a. speed is less than when in glass
|
b. speed is less than before it entered glass
|
|
c. speed is same as that in glass
|
d. speed is same as that before it entered glass
|
|
Answer: D
The speed of a light wave (like any wave) is dependent upon the medium through which it moves. In the case of a light wave, the speed is least in the most dense medium. Thus, the light moves slower in glass than in air. However, upon exiting the glass and entering the air, the light returns to the original speed. The speed is the same for the same medium.
|
[ #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #10 | #11 | #12 | #13 | #14 | #15 | #16 | #17 | #18 | #19 | #20 | #21 | #22 | #23 | #24 | #25 | #26 | #27 | #28 | #29 | #30 | #31 | #32 | #33 | #34 | #35 | #36 | #37 | #38 | #39 | #40 | #41 | #42 | #43 | #44 | #45 | #46 ]
10. Which of the following describes what will happen to a light ray incident on an air-to-glass boundary?
|
a. total reflection
|
b. total transmission
|
|
c. partial reflection, partial transmission
|
d. partial reflection, total transmission
|
|
Answer: C
Upon reaching a boundary, a wave undergoes both reflection and transmission. The only exception is for light in the more dense medium and at angles of incidence greater than the critical angle; in such a case, total internal reflection occurs. Since the question does not specify such conditions, one would have to answer c.
|
[ #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #10 | #11 | #12 | #13 | #14 | #15 | #16 | #17 | #18 | #19 | #20 | #21 | #22 | #23 | #24 | #25 | #26 | #27 | #28 | #29 | #30 | #31 | #32 | #33 | #34 | #35 | #36 | #37 | #38 | #39 | #40 | #41 | #42 | #43 | #44 | #45 | #46 ]
11. Which of the following describes what will happen to a light ray incident on an air-to-glass boundary at an angle of incidence less than the critical angle?
|
a. total reflection
|
b. total transmission
|
|
c. partial reflection, partial transmission
|
d. partial reflection, total transmission
|
|
Answer: C
At a boundary between any two materials, there will be both reflection and transmission. The only exception is when the light is incident in the more dense material and at an incident angle greater than the critical angle.
|
[ #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #10 | #11 | #12 | #13 | #14 | #15 | #16 | #17 | #18 | #19 | #20 | #21 | #22 | #23 | #24 | #25 | #26 | #27 | #28 | #29 | #30 | #31 | #32 | #33 | #34 | #35 | #36 | #37 | #38 | #39 | #40 | #41 | #42 | #43 | #44 | #45 | #46 ]
12. Which of the following describes what will happen to a light ray incident on an glass-to-air boundary at an angle of incidence greater than the critical angle?
|
a. total reflection
|
b. total transmission
|
|
c. partial reflection, partial transmission
|
d. partial reflection, total transmission
|
|
Answer: A
At a boundary between any two materials, there will be both reflection and transmission. The only exception is when the light is incident in the more dense material and at an incident angle greater than the critical angle. Since the light in this problem is in the more dense medium (glass) and at an angle greater than the critical angle, total internal reflection will occur. No transmission will occur at this boundary for such angles.
|
[ #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #10 | #11 | #12 | #13 | #14 | #15 | #16 | #17 | #18 | #19 | #20 | #21 | #22 | #23 | #24 | #25 | #26 | #27 | #28 | #29 | #30 | #31 | #32 | #33 | #34 | #35 | #36 | #37 | #38 | #39 | #40 | #41 | #42 | #43 | #44 | #45 | #46 ]
13. What is the angle of incidence on an air-to-glass boundary if the angle of refraction in the glass (n = 1.52) is 25 degrees?
|
a. 16 degrees
|
b. 25 degrees
|
c. 40 degrees
|
d. 43 degrees
|
|
Answer: C
Use Snell's law:
ni * sine(Theta i) = nr * sine(Theta r)
where
ni =1.52 (in glass), Theta i=25 degrees (angle in glass), nr =1.00 (in air)
Substitute and solve for Theta r.
1.52 * sine(25 degrees) = 1.00 * sine(Theta r)
1.52 * sine(25 degrees) / 1.00 = sine(Theta r)
0.0.6424 = sine(Theta r)
Theta r = invsine(0.6424) = 40.0 degrees
|
[ #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #10 | #11 | #12 | #13 | #14 | #15 | #16 | #17 | #18 | #19 | #20 | #21 | #22 | #23 | #24 | #25 | #26 | #27 | #28 | #29 | #30 | #31 | #32 | #33 | #34 | #35 | #36 | #37 | #38 | #39 | #40 | #41 | #42 | #43 | #44 | #45 | #46 ]
14. A ray of white light, incident upon a glass prism, is dispersed into its various color components. Which one of the following colors experiences the greatest amount of refraction?
|
a. orange
|
b. violet
|
c. red
|
d. green
|
|
Answer: B
The shorter wavelengths of light undergo the most refraction. Thus, violet is refracted the most and red light is refracted the least. The fact that the various component colors of white light refract different amounts leads to the phenomenon of dispersion.
|
15. When light from air hits a smooth piece of glass (n = 1.5) with the ray perpendicular to the glass surface, which of the following will occur?
|
a. reflection and transmission at an angle of 0 degrees
|
b. dispersion
|
|
c. refraction at an angle of 41.8 degrees
|
d. all of the above will occur
|
|
Answer: A
A portion of the light is reflected and a portion of the light is transmitted into the new medium. Since the angle of incidence is 0 degrees, there is no bending of the ray. Noticeable dispersion only occurs when there is refraction of light at two consecutive boundaries which are nonparallel.
|
[ #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #10 | #11 | #12 | #13 | #14 | #15 | #16 | #17 | #18 | #19 | #20 | #21 | #22 | #23 | #24 | #25 | #26 | #27 | #28 | #29 | #30 | #31 | #32 | #33 | #34 | #35 | #36 | #37 | #38 | #39 | #40 | #41 | #42 | #43 | #44 | #45 | #46 ]
16. If total internal reflection occurs at a glass-air surface, then _____.
- no light is refracted
- no light is reflected
- light is leaving the air and hitting the glass with an incident angle greater than the critical angle
- light is leaving the air and hitting the glass with an incident angle less than the critical angle
|
Answer: A
Total internal reflection occurs only when light passes from a more dense medium to a less dense medium (this is why c and d can be ruled out) at an angle of incidence greater than the critical angle. When TIR occurs, all the light is reflected and none of the light is refracted.
|
[ #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #10 | #11 | #12 | #13 | #14 | #15 | #16 | #17 | #18 | #19 | #20 | #21 | #22 | #23 | #24 | #25 | #26 | #27 | #28 | #29 | #30 | #31 | #32 | #33 | #34 | #35 | #36 | #37 | #38 | #39 | #40 | #41 | #42 | #43 | #44 | #45 | #46 ]
17. When light from air hits a smooth piece of glass with the ray perpendicular to the glass surface, the part of the light passing into the glass _____.
|
a. will not change its speed
|
b. will not change its direction
|
|
c. will not change its wavelength
|
d. will not change its intensity
|
|
Answer: B
When the angle of incidence is 0 degrees (as in this case), there is no bending. The ray still slows down and changes its wavelength. A portion of the wave reflects and so there is a change in intensity within the new medium. Yet, there is no refraction or bending; the direction does not change.
|
[ #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #10 | #11 | #12 | #13 | #14 | #15 | #16 | #17 | #18 | #19 | #20 | #21 | #22 | #23 | #24 | #25 | #26 | #27 | #28 | #29 | #30 | #31 | #32 | #33 | #34 | #35 | #36 | #37 | #38 | #39 | #40 | #41 | #42 | #43 | #44 | #45 | #46 ]
For Questions #18 - #20, consider the diagram below.

18. This person suffers from the problem of ____.
|
a. nearsightedness
|
b. farsightedness
|
c. cataracts
|
d. delusions
|
|
Answer: B
A farsighted person has difficulty seeing objects which are placed nearby. The images of nearby objects forms behind the retina as shown in this case. Nearsighted people have the opposite problem in that the images from very distant objects form in front of the retina.
|
[ #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #10 | #11 | #12 | #13 | #14 | #15 | #16 | #17 | #18 | #19 | #20 | #21 | #22 | #23 | #24 | #25 | #26 | #27 | #28 | #29 | #30 | #31 | #32 | #33 | #34 | #35 | #36 | #37 | #38 | #39 | #40 | #41 | #42 | #43 | #44 | #45 | #46 ]
19. This problem could most easily be corrected by the use of a(n) ____.
|
a. converging lens
|
b. diverging lens
|
c. achromatic lens
|
d. good night's sleep
|
|
Answer: A
Since the image of this farsighted individual is forming behind the retina, an artificial lens with increased converging ability will cause the image to form closer to the lens and upon the retina. Farsighted individuals correct for their vision defect through the use of converging lenses.
|
[ #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #10 | #11 | #12 | #13 | #14 | #15 | #16 | #17 | #18 | #19 | #20 | #21 | #22 | #23 | #24 | #25 | #26 | #27 | #28 | #29 | #30 | #31 | #32 | #33 | #34 | #35 | #36 | #37 | #38 | #39 | #40 | #41 | #42 | #43 | #44 | #45 | #46 ]
20. If the image was formed in front of the retina rather than behind the retina, then the person would need to correct the vision problem by using a
|
a. converging lens
|
b. diverging lens
|
c. achromatic lens
|
d. alarm clock
|
|
Answer: B
Nearsighted individuals suffer from an image formed in front of the retina. They must correct for the problem by wearing an artificial lens which provides for some diverging of light prior to reaching the lens of the eye. This will move the image further from the lens of the eye and back towards the retina.
|
[ #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #10 | #11 | #12 | #13 | #14 | #15 | #16 | #17 | #18 | #19 | #20 | #21 | #22 | #23 | #24 | #25 | #26 | #27 | #28 | #29 | #30 | #31 | #32 | #33 | #34 | #35 | #36 | #37 | #38 | #39 | #40 | #41 | #42 | #43 | #44 | #45 | #46 ]
21. Dispersion occurs when _____.
- some materials bend light more than other materials
- a material slows down some colors more than others
- a material changes some colors more than others
- light has different speeds in different materials
|
Answer: B
Dispersion occurs when a single material bends certain colors of light more than other colors of light. The cause is the fact that different colors of light have different speeds within the same material.
|
22. A 3.0 cm tall object is placed along the principal axis of a thin converging lens of 30.0 cm focal length. If the object distance is 40.0 cm, which of the following best describes the image distance and height, respectively?
|
a. 17.3 cm and 7.0 cm
|
b. 120. cm and -9.0 cm
|
c. 17.3 cm and 1.3 cm
|
d. 120. cm and -1.0 cm
|
|
Answer: B
Use the lens equation:
1/di + 1/do = 1/f
where do = 40.0 cm and f = 30.0 cm. Solve for di.
1/di = 1/f - 1/do =1/(30.0 cm) - 1/(40.0 cm) = 0.00833 /cm
di = 1/(0.00833 /cm) = 120. cm
Then use the -di/do = hi/ho to find hi
It is now known that ho = 3.0 cm; do = 40.0 cm; di = 120. cm. Substitute and solve.
hi = -ho *(di/do) = -(3.0 cm) *(120. cm)/(40.0 cm) = -9.0 cm
|
[ #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #10 | #11 | #12 | #13 | #14 | #15 | #16 | #17 | #18 | #19 | #20 | #21 | #22 | #23 | #24 | #25 | #26 | #27 | #28 | #29 | #30 | #31 | #32 | #33 | #34 | #35 | #36 | #37 | #38 | #39 | #40 | #41 | #42 | #43 | #44 | #45 | #46 ]
23. Which of the following best describes the image for a thin converging lens that forms whenever the object is at a distance less than one focal length from the lens?
|
a. inverted, enlarged and real
|
b. upright, enlarged and virtual
|
|
c. upright, reduced and virtual
|
d. inverted, reduced and real
|
|
Answer: B
When an object is located inside of the focal point of a converging lens, the image will be virtual, upright, larger than the object and located on the same side of the lens as the object. In essence, the lens would serve as a magnifying glass.
|
[ #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #10 | #11 | #12 | #13 | #14 | #15 | #16 | #17 | #18 | #19 | #20 | #21 | #22 | #23 | #24 | #25 | #26 | #27 | #28 | #29 | #30 | #31 | #32 | #33 | #34 | #35 | #36 | #37 | #38 | #39 | #40 | #41 | #42 | #43 | #44 | #45 | #46 ]
24. Which of the following best describes the image for a thin diverging lens that forms whenever the magnitude of the object distance is less than that of the lens' focal length?
|
a. inverted, enlarged and real
|
b. upright, enlarged and virtual
|
|
c. upright, reduced and virtual
|
d. inverted, reduced and real
|
|
Answer: C
A diverging lens always produces an image with the same characteristics, regardless of the object distance. The image is always virtual, upright and reduced in size.
|
[ #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #10 | #11 | #12 | #13 | #14 | #15 | #16 | #17 | #18 | #19 | #20 | #21 | #22 | #23 | #24 | #25 | #26 | #27 | #28 | #29 | #30 | #31 | #32 | #33 | #34 | #35 | #36 | #37 | #38 | #39 | #40 | #41 | #42 | #43 | #44 | #45 | #46 ]
25. An object is placed at a distance of 30.0 cm from a thin converging lens along its axis. The lens has a focal length of 10.0 cm. What are the values of the image distance and magnification (respectively)?
|
a. 60.0 cm and 2.00
|
b. 15.0 cm and 2.00
|
c. 60.0 cm and -0.500
|
d. 15.0 cm and -0.500
|
|
Answer: D
Use the lens equation:
1/di + 1/do = 1/f
where do = 30.0 cm and f = 10.0 cm.
Solve for di :
1/di = 1/f - 1/do = 1/(10.0 cm) - 1/(30.0 cm) = 0.0666/cm
di = 1 / (0.0666/cm) = 15.0 cm
Then use the M =-di/do to find M
(do = 30.0 cm; di = 15.0 cm)
Substitute and solve for M:
M = -(15.0 cm) / (30.0 cm) = - 0.500
|
[ #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #10 | #11 | #12 | #13 | #14 | #15 | #16 | #17 | #18 | #19 | #20 | #21 | #22 | #23 | #24 | #25 | #26 | #27 | #28 | #29 | #30 | #31 | #32 | #33 | #34 | #35 | #36 | #37 | #38 | #39 | #40 | #41 | #42 | #43 | #44 | #45 | #46 ]
26. An object is placed at a distance of 6.0 cm from a thin converging lens along its axis. The lens has a focal length of 9.0 cm. What are the values, respectively, of the image distance and magnification?
|
a. -18 cm and 3.0
|
b. 18 cm and 3.0
|
c. 3.0 cm and -0.50
|
d. -18 cm and -3.0
|
|
Answer: A
Use the lens equation:
1/di + 1/do = 1/f
where do = 6.0 cm and f = 9.0 cm.
Solve for di:
1/di = 1/f - 1/do = 1/(9.0 cm) - 1/(6.0 cm) = -0.0556/cm
di = 1 / (-0.0556/cm) = -18 cm
Then use the M =-di/do to find M (do = 6.0 cm; di = -18 cm)
Substitute and solve for M:
M = -(-18 cm) / (6.0 cm) = 3.0
|
[ #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #10 | #11 | #12 | #13 | #14 | #15 | #16 | #17 | #18 | #19 | #20 | #21 | #22 | #23 | #24 | #25 | #26 | #27 | #28 | #29 | #30 | #31 | #32 | #33 | #34 | #35 | #36 | #37 | #38 | #39 | #40 | #41 | #42 | #43 | #44 | #45 | #46 ]
27. An object is placed at a distance of 30.0 cm from a thin converging lens along the axis. If a real image forms at a distance of 10.0 cm from the lens, what is the focal length of the lens?
|
a. 30.0 cm
|
b. 15.0 cm
|
c. 10.0 cm
|
d. 7.50 cm
|
|
Answer: A
Use the lens equation:
1/di + 1/do = 1/f
where do = 6.0 cm and f = 9.0 cm.
Solve for di:
1/di = 1/f - 1/do = 1/(9.0 cm) - 1/(6.0 cm) = -0.0556/cm
di = 1 / (-0.0556/cm) = -18 cm
Then use the M =-di/do to find M (do = 6.0 cm; di = -18 cm)
Substitute and solve for M:
M = -(-18 cm) / (6.0 cm) = 3.0
|
[ #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #10 | #11 | #12 | #13 | #14 | #15 | #16 | #17 | #18 | #19 | #20 | #21 | #22 | #23 | #24 | #25 | #26 | #27 | #28 | #29 | #30 | #31 | #32 | #33 | #34 | #35 | #36 | #37 | #38 | #39 | #40 | #41 | #42 | #43 | #44 | #45 | #46 ]
28. An object is placed at a distance of 40.0 cm from a thin lens along the axis. If a virtual image forms at a distance of 50.0 cm from the lens, on the same side as the object, what is the focal length of the lens?
|
a. 22.2 cm
|
b. 45.0 cm
|
c. 90.0 cm
|
d. 200. cm
|
|
Answer: D
Use the lens equation:
1/di + 1/do = 1/f
where do = 40.0 cm and di = -50.0 cm (Note that di is a negative number since it is a virtual image - i.e., formed on the same side of the lens as the object.)
Solve for f:
1/f = 1/di + 1/do = 1/(-50.0 cm) + 1/(40.0 cm) = 0.00500/cm
f = 1 / (0.00500/cm) = 200. cm
|
[ #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #10 | #11 | #12 | #13 | #14 | #15 | #16 | #17 | #18 | #19 | #20 | #21 | #22 | #23 | #24 | #25 | #26 | #27 | #28 | #29 | #30 | #31 | #32 | #33 | #34 | #35 | #36 | #37 | #38 | #39 | #40 | #41 | #42 | #43 | #44 | #45 | #46 ]
Part B: Multiple-Multiple Choice
29. Which of the following statements are true of converging lenses? Identify all that apply.
- Converging lenses are thicker at the center than they are at the edges.
- If the bottom half of a converging lens is covered, then the top half of the image will not be visible.
- Converging lenses only produce real images.
- Converging lenses can produce images which are both magnified and reduced in size.
- Converging lenses only produce inverted images.
- Converging lenses have a + focal length.
- The images formed by a converging lens can be located on either side of the lens relative to the object.
|
Answer: ADFG
- This is the basic physical feature that characterizes all converging lenses.
- Find a pair of eyeglasses and see if you can test the truth of this statement. Covering half the lens will only have the effect of making the image fainter.
- Converging lenses will produce a virtual image of an object placed in front of F.
- Converging lenses produce magnified images when the object is in front of 2F and reduced images when the object is behind 2F.
- Converging lenses can produce upright images of objects placed in front of F.
- Focal length is + for converging lenses and - for diverging lenses.
- Converging lenses produce both real images formed on the opposite side of the lens (when the object is placed beyond F) and virtual images formed on the same side of the lens (when the object is placed in front of F).
|
[ #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #10 | #11 | #12 | #13 | #14 | #15 | #16 | #17 | #18 | #19 | #20 | #21 | #22 | #23 | #24 | #25 | #26 | #27 | #28 | #29 | #30 | #31 | #32 | #33 | #34 | #35 | #36 | #37 | #38 | #39 | #40 | #41 | #42 | #43 | #44 | #45 | #46 ]
30. Which of the following statements are true of diverging lenses? Identify all that apply.
- Diverging lenses are thicker at the center than they are at the edges.
- If the bottom half of a diverging lens is covered, then the bottom half of the image will not be visible.
- Diverging lenses only produce virtual images.
- Diverging lenses can produce images which are both magnified and reduced in size.
- Diverging lenses only produce upright images.
- Diverging lenses have a - focal length.
- The images formed by a diverging lens can be located on either side of the lens relative to the object.
|
Answer: CEF
- Diverging lenses would be thinner at the center and thickest along the top and bottom edges.
- Just like the case of a converging lens, if half of a diverging lens is covered, the full image is still seen; it is merely fainter.
- Always. A real image is never produced by a diverging lens.
- Diverging lenses only produce one type of image - a virtual image which is upright and reduced in size.
- See above statement.
- Diverging lenses have a - focal length and converging lenses have a + focal length.
- Diverging lenses only produce virtual images; these images are located on the object's side of the lens.
|
[ #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #10 | #11 | #12 | #13 | #14 | #15 | #16 | #17 | #18 | #19 | #20 | #21 | #22 | #23 | #24 | #25 | #26 | #27 | #28 | #29 | #30 | #31 | #32 | #33 | #34 | #35 | #36 | #37 | #38 | #39 | #40 | #41 | #42 | #43 | #44 | #45 | #46 ]
31. Which of the following statements are true of real images? Identify all that apply.
- Real images are inverted.
- Real images as formed by lenses are located on the opposite side of the lens from the object.
- Real images are magnified in size.
- Real images are only formed by converging lenses, never by diverging lenses.
- An image of a real object is formed; the image distance (s' or di) for real images is a + value.
- An image of a real object is formed; the image height (h' or hi) for real images is a + value.
- Real images have a - magnification value.
|
Answer: ABDEG
- This is always the case - real images are inverted and virtual images are upright.
- Real images are always located on the opposite side of the lens; virtual images are located on the object's side of the lens.
- Real images can be either magnified (converging lens, object between F and 2F), reduced (converging lens, object beyond 2F), or the same size (converging lens, object at 2F) as the object.
- Diverging lenses can only produce virtual images; converging lenses can produce both virtual and real images.
- Real images - those formed on the opposite side of the lens have a positive s' value (seep. 789 for more).
- Real images are inverted; this corresponds to a negative h' value.
- Real images are inverted; this corresponds to a negative magnification value.
|
[ #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #10 | #11 | #12 | #13 | #14 | #15 | #16 | #17 | #18 | #19 | #20 | #21 | #22 | #23 | #24 | #25 | #26 | #27 | #28 | #29 | #30 | #31 | #32 | #33 | #34 | #35 | #36 | #37 | #38 | #39 | #40 | #41 | #42 | #43 | #44 | #45 | #46 ]
32. Which of the following statements are true of virtual images? Identify all that apply.
- Virtual images are always upright.
- Virtual images as formed by lenses are always located on the same side of the lens as the object.
- Virtual images are only formed by diverging lenses, never by converging lenses.
- Virtual images are always smaller than the object.
- An image of a real object is formed; the image distance (s' or di) for virtual images is a - value.
- An image of a real object is formed; the image height (h' or hi) for virtual images is a - value.
- Virtual images have a - magnification value.
|
Answer: ABE
- Virtual images, whether formed by mirrors (of any type) or lenses, are always upright; real images are always inverted.
- Virtual images are always located on the object's side of the lens; real images are always located on the opposite side of the lens.
- Virtual images can be formed by both converging lenses (when the object is inside of F) and diverging lenses (regardless of the object location).
- Virtual images can be larger than the object (when formed by converging lenses) or smaller than the object (when formed by diverging lenses).
- Virtual images are located on the object's side of the lens; this corresponds to a negative s' value.
- Virtual images are always upright; this corresponds to a positive h' value.
- Virtual images are always upright; this corresponds to a positive M value.
|
[ #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #10 | #11 | #12 | #13 | #14 | #15 | #16 | #17 | #18 | #19 | #20 | #21 | #22 | #23 | #24 | #25 | #26 | #27 | #28 | #29 | #30 | #31 | #32 | #33 | #34 | #35 | #36 | #37 | #38 | #39 | #40 | #41 | #42 | #43 | #44 | #45 | #46 ]
33. Several characteristics of images are described below. Determine whether these images are real or virtual and whether they are formed by converging, diverging lenses or either type. (In all cases, assume that the object is an upright and real object.)
- Image is upright and magnified.
- Image if upright and reduced in size.
- Image is inverted and magnified.
- Image has a negative s' (di) value.
- Image has a negative h' (hi) value.
- Image has a positive h' (hi) value and a magnification value greater than 1.
|
Answer: See answers below
- Converging only; an upright (and virtual) and magnified image can only be formed when the object is between F and the surface of a converging lens. Diverging lenses would only produce upright images which are reduced in size.
- Diverging only; an upright (and virtual) and reduced image can only be formed by a diverging lens. When converging lenses produce upright images, they are magnified in size.
- Converging only; diverging lenses can only produce upright images which are reduced in size; an inverted and magnified image can be produced by a converging lens when the object is located between F and 2F.
- Both lenses; a negative s' value corresponds to a virtual image; both converging and diverging lenses can produce virtual images.
- Converging only; a negative h' value corresponds to an inverted (and real) image; only a converging lens can produce a real image.
- Converging only; a positive h' value corresponds to an upright (and virtual) image; the M > 1 statement indicates that the image is magnified. A magnified, upright, virtual image can only be produced by a converging lens when the object is between F and 2F.
|
[ #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #10 | #11 | #12 | #13 | #14 | #15 | #16 | #17 | #18 | #19 | #20 | #21 | #22 | #23 | #24 | #25 | #26 | #27 | #28 | #29 | #30 | #31 | #32 | #33 | #34 | #35 | #36 | #37 | #38 | #39 | #40 | #41 | #42 | #43 | #44 | #45 | #46 ]
34. Which of the following statements are true of total internal reflection (TIR)? Include all that apply.
- TIR can only occur when light approaches a boundary and is incident within the most dense media.
- TIR can only occur when the angle of incidence is greater than the critical angle.
- TIR causes a portion of the light to refract along the boundary and the rest to be reflected.
- When TIR occurs, the reflected light follows the law of reflection.
- If TIR occurs at the boundary of water and air, then the light must be within water and heading towards the boundary with air.
- If TIR occurs at the boundary of glass and air, then it is possible that the light is traveling within air and heading towards the glass.
|
Answer: ABE
- There are two conditions which must be met for TIR to occur; this is the first condition.
- This is the second condition.
- When TIR occurs, all (total) of the light reflects. There is no (nada, none, zero, zilch) refraction taking place.
- Yes! Reflection always follows the law of reflection. The angle of incidence equals the angle of reflection.
- TIR can only take place if the light is incident within the more dense of the two medium - in this case, water.
- Never; air is the least dense of the two media; this would violate the first of the two conditions for TIR. TIR would only take place at this boundary if the light was in the glass and heading towards the boundary with air.
|
[ #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #10 | #11 | #12 | #13 | #14 | #15 | #16 | #17 | #18 | #19 | #20 | #21 | #22 | #23 | #24 | #25 | #26 | #27 | #28 | #29 | #30 | #31 | #32 | #33 | #34 | #35 | #36 | #37 | #38 | #39 | #40 | #41 | #42 | #43 | #44 | #45 | #46 ]
Part C: Diagramming and Analysis
|
35. The diagram below shows four incident rays traveling through water (n = 1.33) and approaching the boundary with air (n=1.00). For each incident ray, draw the corresponding reflected ray; then calculate the angle of refraction and draw the corresponding refracted ray. Label or color code your reflected and refracted rays to distinguish them from each other and to match them to the incident ray.
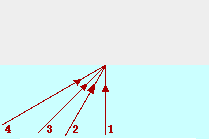
|
Ray
|
Angle of
incidence
|
Angle of
reflection
|
Angle of
refraction
|
|
1
|
0.0 deg.
|
0.0 deg.
|
0.0 deg.
|
|
2
|
30.0 deg.
|
30.0 deg.
|
41.7 deg.
|
|
3
|
45.0 deg.
|
45.0 deg.
|
70.1 deg.
|
|
4
|
60.0 deg.
|
60.0 deg.
|
None
|
|
Answer: See diagram above
The angle of reflection equals the angle of incidence; this is simply the law of reflection. Each angle is measured relative to the normal.
The angle of refraction is determined using Snell's law. For the 30.0-degree angle, the work would be:
nwater * sin(Angle in water) = nair * sin(Angle in air)
1.33 * sin(30.0 deg) = 1.00 * sin(Angle in air)
0.665 = sin(Angle in air)
invsin(0.665) = Angle in air
41.7 deg = Angle in air
The same calculations are done for the other angles to determine the angle of refraction. In the case of the 60.0 degree angle, the mathematics breaks down and the equation cannot be solved for an angle of refraction. This is because refraction does not occur at the water-air boundaries when light is incident in water at angles of incidence greater than the critical angle (approx. 48 degrees).
|
[ #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #10 | #11 | #12 | #13 | #14 | #15 | #16 | #17 | #18 | #19 | #20 | #21 | #22 | #23 | #24 | #25 | #26 | #27 | #28 | #29 | #30 | #31 | #32 | #33 | #34 | #35 | #36 | #37 | #38 | #39 | #40 | #41 | #42 | #43 | #44 | #45 | #46 ]
36. In the diagrams below, construct refracted rays to indicate the direction which the light rays bend upon crossing the boundary.
If light travels faster in medium 1 than in medium 2, then upon entering medium 2, the light will bend towards from the normal.
|
If the index of refraction of medium 1 is greater than medium 2, then upon entering medium 2, the light will bend away from the normal.
|
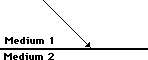
|

|
|
Answer: See diagram above.
On the left, light is moving from a medium in which it travels fast to one in which it travels slow. In such a case, light refracts towards the normal. (Remember fast to slow bends towards as in "FST" or "Freaky Science Teachers".) The refracted ray should be drawn closer to the normal than the incident ray is.
On the right, light is moving from a medium which is more dense or slower to a medium which is less dense or faster. In such a case, light refracts away from the normal. (Remember slow to fast bends away - "SFA" or "Suzie Farts Alot".) The refracted ray should be draw farther away from the normal than the incident ray is.
|
[ #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #10 | #11 | #12 | #13 | #14 | #15 | #16 | #17 | #18 | #19 | #20 | #21 | #22 | #23 | #24 | #25 | #26 | #27 | #28 | #29 | #30 | #31 | #32 | #33 | #34 | #35 | #36 | #37 | #38 | #39 | #40 | #41 | #42 | #43 | #44 | #45 | #46 ]
37. Use Snell's law, a protractor and a straight-edge to trace the path of light through the following objects.
|
Answer: See diagrams above.
Part A
The original incident angle can be measured by drawing a normal at the surface and measuring the angle between the incident ray and the normal; or it can be determined geometrically using the alternating angles theorem. Either way, the incident angle is 45.0 degrees. The refracted angle can be determined using Snell's law (1.00*sin(45.0 deg) = 1.40*sin(theta)); the angle of refraction is 30.3 degrees. The refracted ray at the entry surface can be drawn and traced through the prism to the opposite face of the triangle.
Once reaching the top face of the triangle, the light ray undergoes total internal reflection (TIR). This would have to be first checked by comparing the incident angle to the critical angle. The critical angle for this boundary is 45.6 degrees (invsin(1/1.40)). The incident angle can be measured by drawing the normal or determined geometrically. In either case, the angle of incidence at the top surface is 75.3 degrees. Since this angle is greater than the critical angle, TIR occurs. The ray reflects according to the law of reflection and continues through the prism to the opposite face.
At the right face, the angle of incidence is 30.3 degrees. This can be determined geometrically or by drawing a normal and measuring the angle between the normal and the incident ray. Finally, the angle of refraction of light at this back surface can be computed using Snell's law; the angle is 45.0 degrees (invsin(1.40)sin(30.3 deg))). The exiting light ray can be drawn at an angle of 45.0 degrees from the normal.
Part B
At the entry surface, the light ray approaches with an incident angle of 0 degrees. At this angle, no refraction occurs and the light ray continues across the boundary in its original direction until it reaches the opposite boundary.
The light ray approaches the lower left face of the prism with an angle of incidence of 4.05 degrees (determined geometrically or by drawing a normal and measuring the angle). The critical angle for this boundary is approximately 37 degrees (invsin(1/1.70)). Since the angle of incidence is greater than the critical angle, TIR occurs and the light reflects according to the law of reflection. It then approaches the bottom right face of the prism.
Upon reaching the bottom right face of the prism, the light is incident with an angle of incidence of 45.0 degrees (determined geometrically or by drawing a normal and measuring the angle). Once more, since the angle of incidence is greater than the critical angle, TIR occurs and the light reflects according to the law of reflection. It then approaches the top face of the prism.
The light approaching the top face is traveling along the normal with an angle of incidence of 0 degrees. Similar to the original entry situation, the light will pass across the boundary and exit the prism without any refraction.
Part C
At the entry surface, the light ray approaches with an incident angle of 0 degrees. At this angle, no refraction occurs and the light ray continues across the boundary in its original direction until it reaches the opposite boundary.
At the opposite boundary, the angle of incidence is 45.0 degrees. This can be determined geometrically or by drawing a normal and measuring. The angle of refraction can be determined using Snell's law and the two indices of refraction. The angle of refraction is 35.6 degrees (invsin(1.4*sin(45 deg)/1.70)). The light ray in the second prism enters at a 35.6 degree angle from the normal and continues towards the right face of the prism as shown.
Once reaching the opposite side of the prism, the incident angle can be determined to be 54.4 degrees (determined geometrically or by drawing a normal and measuring the angle). The critical angle for this prism is approximately 36 degrees (invsin(1/1.70)). Since the incident angle is greater than the critical angle, TIR occurs and the light reflects according to the law of reflection. The light approaches the bottom face of the prism.
Once reaching the bottom face of the prism, the angle of incidence is 9.4 degrees (determined geometrically or by drawing a normal and measuring the angle). Using Snell's law, the angle of refraction can be determined to be approximately 16 degrees (invsin(1.7*sin(9.4 deg))). A normal is sketched and the refracted ray out of the prism is drawn at an angle of 16 degrees from the normal.
|
[ #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #10 | #11 | #12 | #13 | #14 | #15 | #16 | #17 | #18 | #19 | #20 | #21 | #22 | #23 | #24 | #25 | #26 | #27 | #28 | #29 | #30 | #31 | #32 | #33 | #34 | #35 | #36 | #37 | #38 | #39 | #40 | #41 | #42 | #43 | #44 | #45 | #46 ]
38. Construct ray diagrams to show where the images of the following objects are located. Draw in the complete image (approximated by an arrow) and describe its characteristics (real or virtual, enlarged or reduced in size, inverted or upright).
|
Answer:
In a ray diagram, pick a point on the extremities of the object and determine where the image of that point is located. Here, the head of the cat is selected and two incident rays and the corresponding refracted rays are drawn. The image point is where they intersect. The same can be done for the other extremity - the feet of the cat (a shortcut is to recognize that the image of an object on the principal axis will be located on the principal axis). Now draw in the complete image between the two image points. Often, the entire process is simplified by considering the object to simply be an arrow. Additional explanation and instruction on drawing ray diagrams is found on another page.
Whenever the object is located beyond the 2F point of a converging lens, the image is located between F and 2F on the other side of the lens; the image is real (located where refracted rays are intersecting), reduced in size, and inverted (and one might add, pretty darn cute).
|
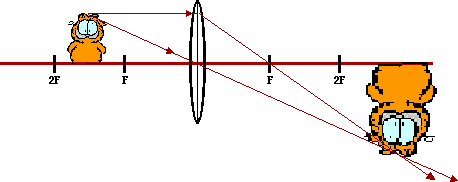 |
| Real |
Magnified |
Inverted |
|
Answer:
In a ray diagram, pick a point on the extremities of the object and determine where the image of that point is located. Here, the head of the cat is selected and two incident rays and their corresponding refracted rays are drawn. The image point is where they intersect. The same can be done for the other extremity - the feet of the cat (a shortcut is to recognize that the image of an object on the principal axis will be located on the principal axis). Now draw in the complete image between the two image points. Often, the entire process is simplified by considering the object to simply be an arrow. Additional explanation and instruction on drawing ray diagrams is found on another page.
Whenever the object is located between the F and the 2F points of a converging lens, the image is located beyond 2F on the other side of the lens; the image is real (located where refracted rays are intersecting), magnified in size, and inverted.
|
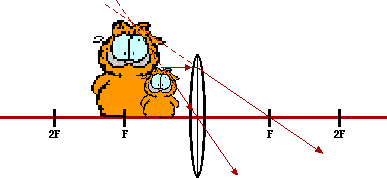
|
|
Virtual
|
Magnified
|
Upright
|
|
Answer:
In a ray diagram, pick a point on the extremities of the object and determine where the image of that point is located. Here, the head of the cat is selected and two incident rays and their corresponding refracted rays are drawn. The image point is where they intersect. In the case, the refracted rays are diverging; the intersection point is found by tracing these refracted rays backwards until they do intersect. The same process can be done for the other extremity - the feet of the cat (a shortcut is to recognize that the image of an object on the principal axis will be located on the principal axis). Now draw in the complete image between the two image points. Often, the entire process is simplified by considering the object to simply be an arrow. Additional explanation and instruction on drawing ray diagrams is found on another page.
Whenever the object is located between the F point and the surface of a converging lens, the image is located on the same side of the lens; the image is virtual (located where refracted rays do not actually exist), magnified in size, and upright.
|
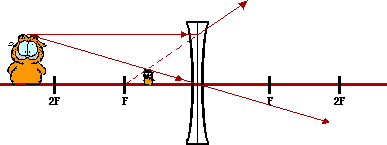
|
|
Virtual
|
Reduced
|
Upright
|
|
Answer:
In a ray diagram, pick a point on the extremities of the object and determine where the image of that point is located. Here, the head of the cat is selected and two incident rays and their corresponding refracted rays are drawn. The image point is where they intersect. In the case, the refracted rays are diverging; the intersection point is found by tracing these refracted rays backwards until they do intersect. The same process can be done for the other extremity - the feet of the cat (a shortcut is to recognize that the image of an object on the principal axis will be located on the principal axis). Now draw in the complete image between the two image points. Often, the entire process is simplified by considering the object to simply be an arrow. Additional explanation and instruction on drawing ray diagrams is found on another page.
Whenever the object is located anywhere in front of a diverging lens, the image is located on the same side of the lens; the image is virtual (located where refracted rays do not actually exist), reduced in size, and upright.
|
[ #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #10 | #11 | #12 | #13 | #14 | #15 | #16 | #17 | #18 | #19 | #20 | #21 | #22 | #23 | #24 | #25 | #26 | #27 | #28 | #29 | #30 | #31 | #32 | #33 | #34 | #35 | #36 | #37 | #38 | #39 | #40 | #41 | #42 | #43 | #44 | #45 | #46 ]
Part D: Problem-Solving
39. The speed of light in a vacuum is 3.00 x 108 m/s. Determine the speed of light through the following materials.
- air (n=1.00)
- ethanol (n=1.36)
- crown glass (n=1.52)
- zircon (n=1.91)
- diamond (n=2.42)
|
Answers:
For each of these questions, find the speed of light in the material by dividing the 3.00 x108 m/s by the index of refraction of the material. This yields the following results:
a. (3.00 x108 m/s)/1.00 = 3 x 108 m/s
b. (3.00 x108 m/s)/1.36 = 2.21 x 108 m/s
c. (3.00 x108 m/s)/1.52 = 1.97 x 108 m/s
d. (3.00 x108 m/s)/1.91 = 1.57 x 108 m/s
e. (3.00 x108 m/s)/2.42 = 1.24 x 108 m/s
|
[ #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #10 | #11 | #12 | #13 | #14 | #15 | #16 | #17 | #18 | #19 | #20 | #21 | #22 | #23 | #24 | #25 | #26 | #27 | #28 | #29 | #30 | #31 | #32 | #33 | #34 | #35 | #36 | #37 | #38 | #39 | #40 | #41 | #42 | #43 | #44 | #45 | #46 ]
 40. Bruno is standing upon the edge of the water with his high-powered laser gun, waiting to zap the next visible fish with a burst of laser light. Frieda deFish, located a distance of 2.17 m out from shore, hopes to hide from view by ducking behind a small lily pad. If Bruno's laser is located 0.850-m above the ground and the lily pad is 1.39 m from shore, then to what depth below the water must Frieda descend in order to be hidden from view? (Given: nwater = 1.33)
40. Bruno is standing upon the edge of the water with his high-powered laser gun, waiting to zap the next visible fish with a burst of laser light. Frieda deFish, located a distance of 2.17 m out from shore, hopes to hide from view by ducking behind a small lily pad. If Bruno's laser is located 0.850-m above the ground and the lily pad is 1.39 m from shore, then to what depth below the water must Frieda descend in order to be hidden from view? (Given: nwater = 1.33)
|
Answer: 0.93 m
This is a problem which involves a combination of right triangle mathematics with Snell's law. As shown in the diagram above, the path of light and other imaginary lines break up the space above and below the water into a couple of right triangles. The game plan involves recognizing that right triangle mathematics must be used to find the angle of incidence and Snell's law can be used to find the angle of refraction. Once the angle of refraction is determined, right triangle trigonometry can be used to find the depth to which Frieda must descend. The two strategic triangles are shown in the diagram below. Angles are labeled to facilitate the discussion that follows.
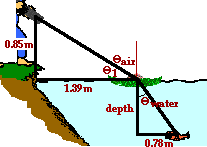
The problem is best solved systematically. Begin by finding theta1 in the diagram. Use the tangent relationship to state that theta1 = invtan(0.850 m/1.39 m) = 31.4 degrees. Since theta1 and the angle of incidence (Thetaair) add up to 90 degrees, the angle of incidence for the light ray approaching the water surface is 58.6 degrees.
Now use Snell's law to determine the angle of refraction. The equation can be set up as follows:
nair • sin(Thetaair) = nwater • sin(Thetawater)
1.00 • sin(58.6 deg) = 1.33 • sin(Thetawater)
1.00 • sin(58.6 deg)/1.33 = sin(Thetawater)
39.9 degrees = Thetawater
Now attention can be turned to the lower triangle and the depth of the fish below the water can be determined. The length of the lower side of the triangle is simply the 2.17 m (distance of the fish from the shoreline) minus the 1.29 m (distance of the lily pad from the shoreline). The tangent function is used to find the side adjacent the 39.9 degree angle.
tan(39.9 degrees) = (0.78 m)/depth
Now using algebra, the equation can be evaluated for the depth:
depth = (0.78 m)/(tan(39.9 deg)) = 0.93 m
|
[ #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #10 | #11 | #12 | #13 | #14 | #15 | #16 | #17 | #18 | #19 | #20 | #21 | #22 | #23 | #24 | #25 | #26 | #27 | #28 | #29 | #30 | #31 | #32 | #33 | #34 | #35 | #36 | #37 | #38 | #39 | #40 | #41 | #42 | #43 | #44 | #45 | #46 ]
 41. Frieda deFish, disturbed at Bruno's militance, pulls out a laser of her own. She temporarily ducks out from her cover and aims it upwards at an angle of 26.5-degrees at Bruno's nose. If Bruno's nose is 1.34-m above the water's edge and if Frieda is a distance of 0.91 m below the water's surface, then how far out from shore must Frieda be to have a direct hit?
41. Frieda deFish, disturbed at Bruno's militance, pulls out a laser of her own. She temporarily ducks out from her cover and aims it upwards at an angle of 26.5-degrees at Bruno's nose. If Bruno's nose is 1.34-m above the water's edge and if Frieda is a distance of 0.91 m below the water's surface, then how far out from shore must Frieda be to have a direct hit?
|
Answer: 1.44 m
Like the problem above, this is a problem which involves a combination of right triangle mathematics with Snell's law. As shown in the diagram above, the path of light and other imaginary lines break up the space above and below the water into a couple of right triangles. Once more, the game plan involves recognizing that Snell's law can be used to find the angle of refraction. Once the angle of refraction is determined, right triangle trigonometry can be used to find the length of the horizontal sides of the two strategic triangles. The two strategic triangles are shown in the diagram below. Angles are labeled to facilitate the discussion that follows.
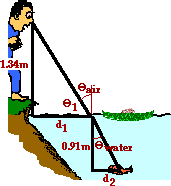
Begin by finding Thetaair in the diagram. This involves the use of Snell's law. The solution is below:
1.33•sin(26.5 deg) = 1.00•sin(Thetaair)
0.5934 = sin(Thetaair)
insin(0.5934) = Thetaair
36.4 degrees = Thetaair
Since Thetaair and Theta1 must add to 90 degrees, Theta1 is 53.6 degrees. This angle can be used to find the length of the horizontal side of the top triangle (d1). The solution involves the use of the tangent function as follows:
tan(53.6 degrees) = (1.34 m)/d1
d1 = (1.34 m)/tan(53.6 degrees)
d1 = 0.988 m
Now attention is focused on the bottom triangle in an effort to determine the length of the horizontal side of the bottom triangle (d2). The tangent function is used and the solution is as follows:
tan(26.5 deg) = d2 /(0.91 m)
d2 =tan(26.5 deg)•(0.91 m)
d2 = 0.45 m
Frieda is a distance of d1 + d2 out from shore. Summing the two distances yields 1.44 m.
|
[ #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #10 | #11 | #12 | #13 | #14 | #15 | #16 | #17 | #18 | #19 | #20 | #21 | #22 | #23 | #24 | #25 | #26 | #27 | #28 | #29 | #30 | #31 | #32 | #33 | #34 | #35 | #36 | #37 | #38 | #39 | #40 | #41 | #42 | #43 | #44 | #45 | #46 ]
42. Determine the critical angle for the following boundaries:
- air - crown glass (n=1.52)
- air - diamond (n=2.42)
- crown glass (n=1.52) - diamond (n=2.42)
- air - Lucite (n=1.40)
- air and a material through which light travels at a speed of 2.10 x 108 m/s
|
Answers:
The critical angle is the angle of incidence at which the angle of refraction is 90.0-degrees. So using Snell's law will result in the following derivation:
ni•sin(Critical Angle) = nr•sin(90 degrees)
sin(Critical Angle) = nr /ni
Critical Angle = invsin(nr/ni)
Since the critical angle only exists for light traveling from the more dense to the less dense medium, the higher n value would be placed in the denominator.
a. Critical angle = invsin(1.00/1.52) = 41.1 degrees.
b. Critical angle = invsin(1.00/2.42) = 24.4 degrees.
c. Critical angle = invsin(1.52/2.42) = 38.9 degrees.
d. Critical angle = invsin(1.00/1.40) = 45.6 degrees.
e. First find the index of refraction using n = (3.00 x 108 m/s) / (2.10 x108 m/s) = 1.42; then use the equation Critical angle = invsin(1.00/1.42) = 44.4 degrees.
|
[ #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #10 | #11 | #12 | #13 | #14 | #15 | #16 | #17 | #18 | #19 | #20 | #21 | #22 | #23 | #24 | #25 | #26 | #27 | #28 | #29 | #30 | #31 | #32 | #33 | #34 | #35 | #36 | #37 | #38 | #39 | #40 | #41 | #42 | #43 | #44 | #45 | #46 ]
43. A lens produces an upright image of an object. The image is reduced in size by a factor of 3.00 when the object is a distance of 16.9 cm from the lens. Determine the focal length.
|
Answer: -8.45 cm
GIVEN:
do = 16.9 cm and hi = (+1/3.00)•ho
Use the magnification equation: M = hi/ho = -di/do = 1/3.00
Using the distance ratio in the magnification equation, it can be shown that
di = -(1/3.00)•do = -(1/3.00) •(16.9 cm) = -5.63 cm
Now use the lens equation to solve for the focal length:
1/f = 1/do + 1/di = 1/(16.9 cm) + 1/(-5.63 cm) = -0.118 / cm
f = 1/-0.118/cm = -8.45 cm
|
[ #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #10 | #11 | #12 | #13 | #14 | #15 | #16 | #17 | #18 | #19 | #20 | #21 | #22 | #23 | #24 | #25 | #26 | #27 | #28 | #29 | #30 | #31 | #32 | #33 | #34 | #35 | #36 | #37 | #38 | #39 | #40 | #41 | #42 | #43 | #44 | #45 | #46 ]
44. A thin lens has a focal point located 19.7 cm from the lens surface. When the object is placed at a specific location, the virtual image it produces is one-fourth the size of the object. Determine the object distance. (Careful of your sign on f.)
|
Answer: 59.1 cm
GIVEN:
f = -19.7 cm and hi = (+1/4) * ho
(Since the image is virtual and reduced, the lens must be a diverging lens; converging lenses produce magnified virtual images.)
Use the magnification equation: M = hi/ho = -di/do = 1/4 to develop an expression for image distance in terms of object distance:
-di/do = 1/4 ---> di = -0.250 * do
Now substitute the expression for image distance into the lens equation to solve for the object distance:
1/(-19.7 cm) = 1/do + 1/(-0.250 * do) = 1/do - 4.00 / do = -3.0 0/ do
do = -(3.00) • (-19.7 cm) = 59.1 cm
|
[ #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #10 | #11 | #12 | #13 | #14 | #15 | #16 | #17 | #18 | #19 | #20 | #21 | #22 | #23 | #24 | #25 | #26 | #27 | #28 | #29 | #30 | #31 | #32 | #33 | #34 | #35 | #36 | #37 | #38 | #39 | #40 | #41 | #42 | #43 | #44 | #45 | #46 ]
45. A thin lens has a focal point located 16.8 cm from the lens surface. Determine the object location which would produce an inverted image which is exactly five times larger than the object.
|
Answer: 20.16 cm
GIVEN:
f = 16.8 cm and hi = (-5.00) * ho
(Since the image is magnified and inverted, the lens must be a converging lens; only converging lenses produce magnified, inverted images. Since the image is inverted, a negative sign is placed into the equation describing the relative heights.)
Use the magnification equation: M = hi/ho = -di/do = -5.00 to develop an expression for image distance in terms of object distance:
-di/do = -5.00 ---> di = 5.00 * do
Now substitute the expression for image distance into the lens equation to solve for the object distance:
1/(16.8 cm) = 1/do + 1/(5.00*do) = 5.00/(5.00*do) + 1.00/(5.00*do) = 6.00/(5.00*do)
do = 1.20 * (16.8 cm) = 20.16 cm
|
[ #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #10 | #11 | #12 | #13 | #14 | #15 | #16 | #17 | #18 | #19 | #20 | #21 | #22 | #23 | #24 | #25 | #26 | #27 | #28 | #29 | #30 | #31 | #32 | #33 | #34 | #35 | #36 | #37 | #38 | #39 | #40 | #41 | #42 | #43 | #44 | #45 | #46 ]
46. A thin lens has a focal point located 16.8 cm from the lens surface. Determine the object location which would produce an upright image which is exactly five times larger than the object.
|
Answer: 13.4 cm
GIVEN:
f = 16.8 cm and hi = (5.00) * ho
(Since the image is magnified and upright, the lens must be a converging lens; only converging lenses produce magnified virtual images. Since the image is upright, a positive sign is placed into the equation describing the relative heights.)
Use the magnification equation: M = hi/ho = -di/do = 5.00 to develop an expression for image distance in terms of object distance:
-di/do = 5.00 ---> di = -5.00 * do
Now substitute the expression for image distance into the lens equation to solve for the object distance:
1/(16.8 cm) = 1/do + 1/(-5.00 * do) = 5.00 / (5.00*do) - 1/(5.00*do) = 4.00 / (5.00*do)
do = 4.00 / 5.00 • (16.8 cm) = 13.4 cm
|
[ #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #10 | #11 | #12 | #13 | #14 | #15 | #16 | #17 | #18 | #19 | #20 | #21 | #22 | #23 | #24 | #25 | #26 | #27 | #28 | #29 | #30 | #31 | #32 | #33 | #34 | #35 | #36 | #37 | #38 | #39 | #40 | #41 | #42 | #43 | #44 | #45 | #46 ]
Navigate to:
Review Session Home - Topic Listing
Refraction and Lenses - Home || Printable Version || Questions with Links
Answers to Questions: All || #1-#20 || #21-#34 || #35-#46
You Might Also Like ...
Users of The Review Session are often looking for learning resources that provide them with practice and review opportunities that include built-in feedback and instruction. If that is what you're looking for, then you might also like the following:
- The Calculator Pad
The Calculator Pad includes physics word problems organized by topic. Each problem is accompanied by a pop-up answer and an audio file that explains the details of how to approach and solve the problem. It's a perfect resource for those wishing to improve their problem-solving skills.
Visit: The Calculator Pad Home | Calculator Pad - Refraction and Lenses
- Minds On Physics the App Series
Minds On Physics the App ("MOP the App") is a series of interactive questioning modules for the student that is serious about improving their conceptual understanding of physics. Each module of the series covers a different topic and is further broken down into sub-topics. A "MOP experience" will provide a learner with challenging questions, feedback, and question-specific help in the context of a game-like environment. It is available for phones, tablets, Chromebooks, and Macintosh computers. It's a perfect resource for those wishing to refine their conceptual reasoning abilities. Part 6 of the series includes topics in Refraction and Lenses.
Visit: MOP the App Home || MOP the App - Part 6