|
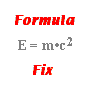
|
The electric field strength (E) at a given location about a source charge is dependent upon the quantity of charge on the source charge (Q) and the distance that the location is from the source (d). The dependency between electric field strength, the quantity of charge on the source charge, and the distance from the source is expressed by the equation
E = k • Q / d2
|
|
|
Equations such as the one shown in the Formula Fix section are often used as algebraic recipes for problem-solving. But equations can also be powerful guides for thinking about how a variation in one variable would affect another variable. In this question, we have to think about how a variation in d affects the E. The question can be answered by thinking in terms of factors of change. According to the equation, the electric field strength depends inversely on the square of this change. Whatever change is made in d, the inverse change is made in E. And the factor by which the change is made of E is the square of the factor by which the d changes.
In this question, the distance is increased by a factor of three. That is, the new distance is three times bigger than the original distance. Thus, E is decreased by a factor of 32. The new electric field strength is nine times smaller than (or one-ninth) the original electric field strength.
|