Vectors and Forces in 2D: Extra Problems
The problems below are provided as additional problems to
the original set of 27 Vectors and Forces in 2-D problems. Just like problems in the original set, these problems consist of a problem, an answer (revealed by clicking a link), an audio guided solution, and links to an
Overview page of formulas and to The Physics Classroom Tutorial pages. The Extra Problems pertain to various aspects of the topic of vectors, vector addition, vector resolution, vector components, Newton's second law, angled forces, equilibrium, and inclined planes. The additional problems are grouped into three sets of 20 problems each.
Problem Set A
 Problem 1:
Problem 1:
A man is attempting to train his dog as shown in the diagram at the right. He is pulling on the dog with a force of 58.7 Newtons at an angle of 33.7 degrees above the horizontal. Find the x-component of the applied force (in Newtons).
View Audio Solution.
Problem 2:
(Referring to the previous problem.) Find the y-component of the applied force (in Newtons).
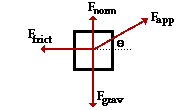 Problem 3:
Problem 3:
Consider the free-body diagram shown at the right. If the applied force is 99.1 N at an angle of 33.0 degrees, the force of gravity is 83.3 N and the coefficient of friction is 0.375, then what is the acceleration (in m/s/s) of the object. Indicate the direction as right or left.

Problem 4:
Consider the free-body diagram shown at the right. If the applied force is 99.1 N at an angle of 23.0 degrees, the force of gravity is 83.3 N and the coefficient of friction is 0.375, then what is the acceleration (in m/s/s) of the object. Indicate the direction as right or left.

Problem 5:
Consider the free-body diagram shown at the right. The object's mass is 12.6 kg. An applied force of 53.7 N is exerted at an angle of 26.5 degrees with the horizontal. What coefficient of friction would result in the object moving with a constant velocity of 1.06 m/s?
Problem 6:
On takeoff, the combined action of the engines and the wings of an airplane exerts a force of 8607 N on the plane upward at an angle of 21.4 degrees above the horizontal. The plane rises with a constant velocity in the vertical direction while continuing to accelerate in the horizontal direction. What is the weight (in Newtons) of the plane?
Problem 7:
(Referring to the previous problem.) What is the horizontal acceleration (in m/s/s) of the plane?
Problem 8:
A box of books weighing 286 N is shoved across the floor of an apartment by exerting a force of 412 N downward at angle of 35.2 degrees below the horizontal . If the coefficient of kinetic friction is 0.505, how long (in seconds) does it take the box to move 2.13 meters.
Problem 9:
A man doing his spring cleaning pulls a 139-N vacuum cleaner across the floor at a constant velocity of 1.03 m/s by exerting a force on it at an angle of 31.5 degrees above the horizontal. If he must pull with a force of 30.8 N to move the vacuum cleaner, what is the coefficient of friction between the vacuum clearner and the floor?
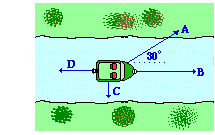 Problem 10:
Problem 10:
Four forces (labled A, B, C, and D) act upon a boat as shown in the diagram at the right. Find the magnitude of the resultant force (in Newtons). Given: A = 2056 N; B = 2721 N; C = 737 N; D = 454 N.
Problem 11:
(Referring to the previous problem.) Find the direction (in degrees, counter-clockwise from East) of the resultant force.
Problem 12:
A student slides a 1162 N crate across the floor by pulling with a force of 702 N at an angle of 27.3 degrees with the horizontal. If the crate moves at a constant speed, find the coefficient of sliding friction between the crate and the floor.
Problem 13:
A 30.8-kg sign is hanging symmetrically by two cables which make an angle of 19.8 degrees with the horizontal. How much vertical pull (in Newtons) must a single cable supply in order to balance the weight of the sign?
Problem 14:
(Referring to the previous problem.) Determine the tension (in Newtons) in one of the cables.
 Problem 15:
Problem 15:
It is amateur night at the tightrope walker's convention, and a 571-N performer finds himself in the awkward position shown in the diagram at the right. The angle between the rope and the horizontal is 9 degrees. Determine the tension (in Newtons) in the cable.
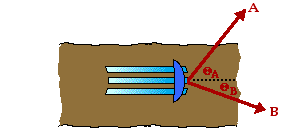 Problem 16:
Problem 16:
Two horses are pulling a sled along an icy road; assume that friction between the sled and the road is negligible. A farmer keeps the sled along the proper path by pulling on it with a rope attached at the point where the cables from the horses are attached. The noise startles the horses and they move towards opposite sides of the road as shown in the diagram at the right (a top view). What is the magnitude of the force (in Newtons) that the farmer will have to exert on the sled to keep it moving along the road at constant velocity? Given: Force A = 671 N; Force B = 461 N; Theta A = 51.5 degrees; Theta B = 20.9 degrees
Problem 17:
(Referring to the previous problem.) What is the direction of the force (in degrees, counter-clockwise from East) that the farmer exerts to keep the sled moving in the original direction at a constant speed?
Problem 18:
A 130-N light fixture is hung by two cables which make an angle of 53.3 degrees with the horizontal. Find the tension (in Newtons) in the two cables. (NOTE: The tension is the same in each cable; merely enter the tension of one of the cables.)
Problem 19:
In the Eat at Ed's lab, a sign is hung symmetrically by a light string. The string makes a V-shape due to the downward pull of the sign. The angle between the string (i.e., the angle of the V) is 96 degrees. The tension on each side of the string is 14 N. Determine the mass (in kg) of the sign.
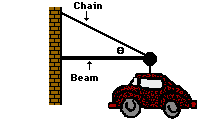 Problem 20:
Problem 20:
An automobile dealership has chosen to hang a car outside the entry to their showroom. The car's mass is 1050 kg. The car's weight will be supported by a heavy-duty chain which pulls upwards and leftwards. A beam will push outward to balance the inward pull of the chain. The manufacturer of the chain claims it has a breaking strength of 32200 Newtons. Village code requires that there be a safety factor of 2.2. That is, the actual tension in the chain must be no more than 1 / 2.2 of the breaking strength. What is the minimum angle (in degrees) at which the dealership can hang the car?
Problem Set B
Problem 1:
A furniture crate of mass 58.5 kg is at rest on a loading ramp that makes an angle of 24.8 degrees with the horizontal. The coefficient of kinetic friction between the ramp and the crate is 0.252. What force, (in Newtons) applied parallel to the ramp, is required to push the crate up the incline at a constant speed?
Problem 2:
A shopper pushes a 38.8-kg cart up a 21.3-degree smooth ramp, What force (in Newtons), directed along the incline, must the shopper exert to give the cart an acceleration of 0.655 m/s/s?
Problem 3:
A box slides down a 31.3-degree ramp with an acceleration of 1.22 m/s/s. Determine the coefficient of kinetic friction between the box and the ramp.
Problem 4:
A box weighing 5425 N is being pulled up an inclined plane that rises 2.02 m for every 7.63 m of length measured along the incline. If the coefficient of friction is 0.573, determine the force (in Newtons), applied parallel to the incline, necessary to move it up the incline at constant speed.
Problem 5:
A crate is held at rest on a frictionless 51.6-degree ramp by a rope parallel to the incline. If the tension in the rope is 6896 N, then what is the mass of the crate (in kg)?
Problem 6:
A 38.8-kg wagon is towed up a hill which is inclined at 18.5 degree with respect to the horizontal. The tow rope is parallel to the incline and has a tension of 138 N in it. Assume that the wagon starts from rest at the bottom of the hill and neglect friction. How fast (in m/s) is the wagon going after moving 63.9-meters up the hill?
Problem 7:
Box A has a mass of 51.3 kg and is on top of a frictionless surface inclined at 24.4 degrees. Box B has a mass of 27.5 kg and is on top of a second frictionless surface inclined at the same angle. Both boxes accelerate down their inclines. How many times greater is the acceleration of Box A than Box B?
Problem 8:
A car is at rest at the top of a driveway that has a slope of 14.4 degrees. If the brake of the car is released, find the acceleration (in m/s/s) of the car down the driveway.
Problem 9:
(Referring to the previous problem.) Find the time (in seconds) it takes the car to reach the street 8.39 m away (as measured along the incline).
Problem 10:
A boy drags a 117-N sled up a 19.55 degree slope at constant velocity. If the coefficient of friction between the sled and hill is 0.269, what force (in Newtons) must he exert at an angle of 35 degrees with the hill?
Problem 11:
In order to determine the coefficients of friction between rubber and various surfaces, a student uses a rubber eraser and an inclined board. In one experiment, the eraser slips down the incline when the angle of inclination is 26.7 degrees, and then moves down the incline with a constant speed when the angle is reduced to 22.5 degrees. Determine the coefficient of static friction for this experiment.
Problem 12:
(Referring to the previous problem.) Determine the coefficient of kinetic friction for this experiment.
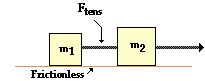 Problem 13:
Problem 13:
Two blocks are connected by a light string and pulled across a horizontal, frictionless surface as shown in the diagram at the right. Their masses are 11.0 kg (m1) and 22.0 kg (m2). A force of 102-N is applied to the 22.0-kg block (m2). Determine the acceleration (in m/s/s) of the system of two blocks.
Problem 14:
(Referring to the previous problem.) Determine the tension (in Newtons) in the string which connects the two blocks.
Problem 15:
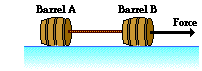 Two barrels, of masses 4.0 kg (Barrel A) and 8.0 kg (Barrel B) are pulled across the frictionless surface of a frozen pond by an ice fisherman. If he exerts a force of 23 N on the lead barrel (Barrel B) as shown in the diagram at the right, then determine the acceleration (in m/s/s) of the system of two barrels.
Two barrels, of masses 4.0 kg (Barrel A) and 8.0 kg (Barrel B) are pulled across the frictionless surface of a frozen pond by an ice fisherman. If he exerts a force of 23 N on the lead barrel (Barrel B) as shown in the diagram at the right, then determine the acceleration (in m/s/s) of the system of two barrels.
Problem 16:
(Referring to the previous problem.) What is the tension (in Newtons) in the cord connecting the two barrels?
Problem 17:
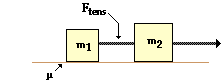 Two blocks are connected by a light string as shown in the diagram at the right. Their masses are 11.0 kg (m1) and 22.0 kg (m2). A force of 102-N is applied to the 22.0-kg block (m2). The coefficient of friction between the blocks and the surface is 0.134. Determine the acceleration (in m/s/s) of the each block.
Two blocks are connected by a light string as shown in the diagram at the right. Their masses are 11.0 kg (m1) and 22.0 kg (m2). A force of 102-N is applied to the 22.0-kg block (m2). The coefficient of friction between the blocks and the surface is 0.134. Determine the acceleration (in m/s/s) of the each block.
Problem 18:
(Referring to the previous problem.) Determine the tension (in Newtons) in the string which connects the two blocks.
Problem 19:
A tractor is pulling two logs in tandem. The logs are fastened together by a chain. Each log weighs 1680 N, and the logs are moving with a constant velocity. The tractor exerts a force of 1611 N on the front log, and this same log is acted on by a force of friction of 882 N. Determine the tension (in Newtons) in the chain between the two logs.
Problem 20:
(Referring to the previous problem.) Determine the force of friction (in Newtons) on the back log.
Problem Set C
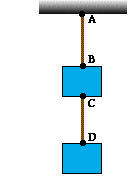
Problem 1:
Two blocks are held together by a rope and attached to the ceiling of an elevator by a second rope (see diagram). The mass of the top block is 14.0 kg; the mass of the bottom block is 10.4 kg. The elevator accelerates upwards at 2.84 m/s/s. Find the tension (in Newtons) in the top rope (connecting points A and B).
Problem 2:
Find the tension (in Newtons) in the bottom rope (connecting points C and D).
Problem 3:
A 8412-kg tow truck pulls a 2686-kg car horizontally into a garage. If the motor of the tow truck exerts a forward thrust on the truck of 780 N, what is the tension (in Newtons) in the cable connecting the truck to the car? (Neglect any forces of friction.)
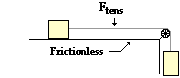 Problem 4:
Problem 4:
An 8.0-kg mass resting on a smooth horizontal table is connected to a cable that passes over a pulley and then is fastened to a hanging 12.2-kg mass. See diagram. Find the acceleration (in m/s/s) of the two objects.
Problem 5:
(Referring to the previous problem.) Find the tension (in Newtons) in the string connecting the two masses.
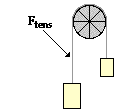 Problem 6:
Problem 6:
Two masses of 3.8 kg and 6.0 kg are connected by a light string that passes over a frictionless pulley as shown in the diagram at the right. Determine the tension (in Newtons) in the string.
Problem 7:
(Referring to the previous problem.) Determine the acceleration (in m/s/s) of the two-mass system.
Problem 8:
(Referring to the previous problem.) Determine the distance (in meters) the two masses will move in the first 1.52 seconds of motion.
Problem 9:
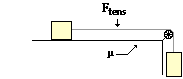 A 8-kg mass resting on a horizontal table is connected to a cable that passes over a pulley and then is fastened to a hanging 12.2-kg mass. See diagram. The coefficient of friction between the 8-kg mass and the table is 0.286. Find the acceleration (in m/s/s) of the two objects.
A 8-kg mass resting on a horizontal table is connected to a cable that passes over a pulley and then is fastened to a hanging 12.2-kg mass. See diagram. The coefficient of friction between the 8-kg mass and the table is 0.286. Find the acceleration (in m/s/s) of the two objects.
Problem 10:
 A 1422-kg car is on an inclined plane inclined at an angle of 30.0 degrees. A cable is connected to the car, stretched over a pulley at the end of the incline and connected to a 11809-N counterweight. See diagram. Determine the acceleration (in m/s/s) of the car. Also indicate the directon of acceleration. (Ignore any effects of friction.)
A 1422-kg car is on an inclined plane inclined at an angle of 30.0 degrees. A cable is connected to the car, stretched over a pulley at the end of the incline and connected to a 11809-N counterweight. See diagram. Determine the acceleration (in m/s/s) of the car. Also indicate the directon of acceleration. (Ignore any effects of friction.)
Problem 11:
(Referring to the previous problem.) Determine the tension (in Newtons) in the cable.
Problem 12:
(Referring to the previous problem.) What mass (in kg) should the counterweight have in order for the car to move down the incline at an acceleration of 2.10 m/s/s?
Problem 13:
A 2-mass system is established as shown in the animation (use button below). A 2.00-kg mass is sliding on a surface inclined at an angle of 51.2 degrees. The hanging mass is allowed to drop from rest. It takes 1.36 seconds for the hanging mass to fall through 1.98 meters and hit the ground. The coefficient of friction between the surface and the sliding mass is 0.324. What is the mass (in kg) of the hanging mass?
Problem 14:
A hanging 2.0-kg block begins to accelerate a 4.1-kg block on a horizontal surface. But a rope connected to the wall at 35.8 degrees brings the block to an equilibrium position. What is the tension (in Newtons) in the angled rope that is required to keep the block from accelerating? The coefficient of friction between the surface and the 4.1-kg block is 0.23.
Problem 15:
A person walks into an elevator holding two masses hanging on ropes, one below the other. The top mass is 5.20 kg and the lower mass is 3.40 kg. The elevator begins to move downward with an acceleration of 5.05 m/s/s before reaching a constant velocity. How much tension (in Newtons) is in the rope between the masses during the acceleration?
Problem 16:
Three forces push on a 90.0 Newton object at once. One force of 41.0 Newtons at 30.0 degrees, a second force of 19.0 Newtons at 180 degrees and a third force of 16.0 Newtons at 240.0 degrees. (All directions are given as a counter-clockwise angle of rotation from due East.) If the object starts at rest, how fast (in m/s) will it be moving in 19.0 seconds?
Problem 17:
A 12.8 kg box rests on a frictionless surface. The box is pulled at an angle of 20 degrees with a force of 43.2 Newtons. If the force acts over a distance of 44.0 meters, What is the box's final velocity (in m/s)?
Problem 18:
An airboarder is falling and experiencing an increasing air resistance force until terminal velocity is reached. If the 66.4-kg airboarder experiences a downward acceleration of 4.92 m/s/s at a certain point in time, what is the air resistance force (in Newtons) at that instant?
Problem 19:
A 68.8-kg skiier heads down a frictionless slope from rest on an incline of 32.8-degrees. If the hill is 50.4 meters high on the vertical, what is the skiier's final velocity (in m/s) at the bottom? Ignore air resistance.
Problem 20:
James Bond is traveling in his car at 25.2 m/s when Mr. Goldfinger grabs onto the back of his car. Bond's car produces a forward force of 10809 Newtons while Mr. Goldfinger's car snatcher pulls on Bond's car with a force of 16213 Newtons. Determine the velocity (in m/s) of Bond's car (1500 kilograms including Bond himself) 28.0 seconds later. Also indicate the direction of velocity.