Work and Energy: Extra Problems
The problems below are provided as additional problems to
the original set of 32 Work and Energy problems. Just like problems in the original set, these problems consist of a problem, an answer (revealed by clicking a link), an audio guided solution, and links to an
Overview page of formulas and to The Physics Classroom Tutorial pages. The Extra Problems pertain to various aspects of the topic of work, energy, power, the work-energy relationship, and the conservation of mechanical energy. The problems are divided into six separate sets of problems. The difficulty of the problems increase as one progresses to each subsequent problem set.
Problem Set A
Problem 1:
A rightward force of 159 N is applied to a 47.4-kg object to displace it to the right for a distance of 2.44 meters. Determine the work (in Joules) done upon the object.
Problem 2:
Renatta Gass applies a rightward force of 519 Newtons to her 1059 kg car to displace it rightward across the ice. She does a total of 37443 Joules of work on the car. Determine the displacement (in meters) of the car.
Problem 3:
A 3.19-kg object is tied to a rope and lifted vertically upward at a constant speed of 1.2 m/s for a displacement of 21.4 m. Determine the work (in Joules) done upon the object.
Problem 4:
Hans Full is pulling on a rope to drag his backpack to school across the ice. He pulls upwards and rightwards with a force of 22.9 Newtons at an angle of 35.0 degrees to drag his backpack a horizontal distance of 129.7 meters to the right. Determine the work (in Joules) done upon the backpack.
Problem 5:
Anna Litical is doing the It's All Uphill Lab. She applies a 12.9-Newton force parallel to the inclined plane in order to pull a cart up a hill inclined at an angle of 38.0 degrees. If she drags the cart a distance of 114.8 cm, then how much work (in Joules) does she do upon the cart?
Problem 6:
A 329.7 gram squirrel does 28 pushups, displacing itself by a distance of 10.7 cm for each pushup. Determine the total work (in Joules) done on the squirrel while moving upward. (Enter your answer accurate to the third decimal place. Avoid rounding until the end.)
Problem 7:
Jack runs up the stairs, elevating his 64.4 kg body a vertical distance of 2.14 meters in a time of 1.22 seconds. Determine the power (in Watts) done by the stairs on Jack's body.
Problem 8:
During peak shopping season at Northbrook Court, an escalator elevates 1148 passengers a vertical distance of 8.28 meters over the course of 22.9 minutes. If the average mass of the passengers are 51.4 kg, determine the power (in Watts) delivered by the escalator to the people.
Problem 9:
The motor of a freight elevator is rated at 13.1 kW. With what maximum speed (in m/s) would it be able to lift a 114-kg load?
Problem 10:
A toe rope is being used to toe 18 skiiers up a ski hill at a constant speed. The average mass of the skiiers is 49.8 kg. The hill is inclined at 11.4 degrees. The power output of the motor is 3.44 kW. With what maximum speed (in m/s) can the skiier be toed? Assume that there is negligible friction.
Problem 11:
A 54.4-kg baserunner begins his/her slide into second base when moving at a speed of 4.59 m/s. The coefficient of friction between his clothes and the earth is .629. How much work (in Joules) is done on the runner as he/she slides to a stop?
Problem 12:
A horizontal force of 42.9 Newtons is used to push a 21.4-kg packing crate on a rough horizontal surface through a distance of 41.4 meters. If the crate moves at a constant speed, then determine the work (in Joules) done by the friction force
Problem 13:
A stewardess pulls her 47.4-N flight bag a distance of 98.9 m along an airport floor at constant speed. The force she exerts is 36.4 N at an angle of 39.4 degrees above the horizontal. Determine the work (in Joules) which she does on the flight bag.
Problem 14:
A 1159-kg car accelerates uniformly from rest to a speed of 11.4 m/s in 3.29 seconds. Determine the average power (in hp) delivered by the engine during these 3.29 seconds. (1 hp = 746 W)
Problem 15:
An elevator having a mass of 129 kg starts upward from rest. It moves upward for 3.29 s with constant acceleration until reaching its final cruising speed of 2.44 m/s. What is the average power (in W) of the elevator motor during this time period?
Problem Set B
Problem 1:
A 1248-kg car is moving at 42.6 mi/hr. If the car brakes to a stop, then how much heat (in Joules) will be lost through friction in the brake linings? Enter a positive value. (1609 m = 1 mi)
Problem 2:
A very good major league baseball pitcher can throw a baseball at 109.3 mi/h, while an ordinary Little League pitcher can throw the ball at a speed of about 52.4 mi/h. If the baseball has a mass of 0.144 grams, find how many times greater is the kinetic energy of the faster ball than that of the slower ball.
Problem 3:
A 1186-kg vehicle is moving along a horizontal surface with a speed of 20.5 m/s. What work (in J) must be done on the car by the brakes to bring this car to rest in 5.48 seconds?
Problem 4:
A mechanic pushes a 1872-kg car from rest to a speed of v, doing 4372 J of work in the process. Neglecting resistive forces, determine the final speed, v (in m/s) of the car.
Problem 5:
What is the gravitational potential energy (in J) relative to the ground of a .248-kg ball at the top of a 96.7-m tall building?
Problem 6:
A 1.87-kg ball hangs at the end of a string 1.55 m in length from the ceiling of a room. The height of the room is 3.24 m. What is the gravitational potential energy (in J) of the ball relative to the floor?
Problem 7:
A 1.68-g bullet leaves the barrel of a gun at a speed of 324 m/s. If the length of the barrel is 66.7 cm, then determine the average force (in N) exerted by the expanding gases on the bullet as it moves the length of the barrel.
Problem 8:
A 1901-kg car moves down a level highway under the action of two forces. One is a forward force on the car of 1309 N from the motor; the second force is a 772-N resistive force. Use the work-energy theorem to find the speed of the car (in m/s) after it has moved a distance of 18.6 m, assuming it starts from rest.
Problem 9:
A 948-kg roller coaster car is initially at the top of a rise (point A). It then moves 136 feet at an angle of 57.4 degrees below the horizontal to a lower point (point B). Find the net force acting upon the coaster along the slope and use it to determine the work done (in J) as it moves from point A to point B. (3.28 feet = 1.00 m)
Problem 10:
A 7.86-kg sled is given a kick on a frozen pond, imparting to it an initial speed of 1.92 m/s. The coefficient of friction between the sled and the ice is 0.140. Use the work-energy theorem to determine the distance (in m) the sled moves before coming to rest.
Problem 11:
A 30.2-N child is in a swing attached to ropes which are 2.30 m long. Find the gravitational potential energy (in J) of the child relative to its lowest point if the swing is pulled back such that the cables make a 29.2 degree angle with the vertical.
Problem 12:
Li Ping Phar, the esteemed Chinese ski jumper, has a mass of 48.0 kg. He is moving with a speed of 23.4 m/s at a height of 44.6 meters above the ground. Determine the total mechanical energy (in J) of Li Ping Phar.
Problem 13:
A 0.179 kg ball is moving upward with a speed of 55.9 m/s when at a height of 86.1 meters above the ground. Determine the total mechanical energy (in J) of the ball.
Problem 14:
A worker applies a 210. N force to pull a 37.1 kg object along an inclined plane to a height of 3.66 m at a constant speed. What is the increase in potential energy (in J) of the object?
Problem Set C
Problem 1:
A car is moving across a level highway with a kinetic energy of 137646 Joules. The brakes are applied and the wheels become locked as the 875-kg car slows to a stop over 5.56 seconds. Determine the work (in Joules) done upon the car.
Problem 2:
A skier is moving along a plateau of a ski slope with a kinetic energy of 6376 Joules and a potential energy of 10752 Joules (relative to the bottom of the slope). If the skier has a kinetic energy of 22752 Joules at the bottom of the slope, then what quantity of work (in Joules) was done upon the skier by use of the poles?
Problem 3:
A volleyball approaches a GBS spiker with a kinetic energy of .475 Joules and a potential energy of 1.376 Joules. If the ball has a kinetic energy of 4.376 Joules as it strikes the ground, then what quantity of work (in Joules) does the spiker do upon the ball?
Problem 4:
A 168-gram baseball is moving with a kinetic energy of 43.4 Joules and a potential energy of 49.7 Joules at one location in its trajectory. If the effect of air resistance on the baseball can be ignored, then what is its kinetic energy (in Joules) the instant prior to striking the ground?
Problem 5:
A bowling ball is attached by a 2.59-meter cable to the ceiling. It has 10.9 Joules of potential energy when held at a height of 4 feet above the ground. It is released from rest allowed to swing as a pendulum. Determine its kinetic energy (in Joules) when it is at a height of 1 foot above the ground.
Problem 6:
Pete Zaria applies a rightward force of 1.37 Newtons over a distance of .575 meters to set a 656 gram root beer mug from rest into motion along a level countertop. Determine the kinetic energy (in Joules) of the root beer mug after Pete is done pushing it.
Problem 7:
Esteemed Chinese ski jumper, Li Ping Phar, leaves the jump ramp with a kinetic energy of 16882 Joules and a potential energy (relative to the bottom of the ski hill) of 13505 Joules. She encounters -2094 Joules of work due to air resistance during her flight through the air. Determine her kinetic energy (in Joules) the instant prior to striking the ground at the bottom of the hill.
Problem 8:
Mr. Henderson's Fiat is in the auto shop. A machine does 12752 Joules of work to hoist the car up to a height of 1.63 meters. Determine the mass (in kg) of the Fiat.
Problem 9:
A 168-gram baseball is moving with a kinetic energy of 43.4 Joules and a potential energy of 49.7 Joules at one location in its trajectory. If the effect of air resistance on the baseball can be ignored, then what is its speed (in m/s) the instant prior to striking the ground?
Problem 10:
A 656-kg roller coaster car is lifted to a height of 48.7 meters above the ground where it begins its descent from an initial rest position. If -10941 Joules of work are done on the car as it descends the first hill to ground level, then what is its kinetic energy (in Joules) at the bottom.
Problem 11:
A 2.37 kg physics cart starts from rest at the top of a .637-meter high incline. Due to air resistance, 4.56 percent of its total energy is lost during its descent down the hill. Determine the kinetic energy (in Joules) of the cart at the bottom of the hill.
Problem 12:
A 337.6 gram ball is moving along the ground with a speed of 2.18 m/s. It approaches a hill inclined at 16.8 degrees to the horizontal. What potential energy (in Joules) will the ball have when it reaches the peak of its path up the incline? (Ignore any effects of rotation or friction.)
Problem 13:
Esteemed Chinese ski jumper, Li Ping Phar, leaves the jump ramp with a kinetic energy of 16882 Joules and a potential energy (relative to the bottom of the ski hill) of 13505 Joules. She encounters -2094 Joules of work due to air resistance during her flight through the air. Determine the speed (in m/s) of her 49.2-kg body the instant prior to striking the ground at the bottom of the hill.
Problem 14:
A 456-kg roller coaster car is moving with a speed of 15.8 m/s at the top of a 16.7-meter high loop. What is the kinetic energy (in Joules) of the car at the bottom of the loop?
Problem Set D
Problem 1:
A baseball player decides to show his skills by catching a 0.142-kg baseball dropped from the top of a 96.0-m tall building. What is the speed (in m/s) of the baseball just before it strikes his glove?
Problem 2:
A child and sled with a combined mass of 35.9 kg slide down a frictionless hill. The sled starts from rest and has acquired a speed of 3.70 m/s by the time it reaches the bottom of the hill. What is the height (in m) of the hill?
Problem 3:
A 39.3-kg high jumper leaves the ground with a speed of 5.70 m/s. How high (in m) can he leap?
Problem 4:
A baseball player throws a baseball straight up into the air with an initial speed of 21.9 m/s. Find the speed of the ball (in m/s) when it is halfway up to its maximum height.
Problem 5:
Tarzan swings on a vine 28.2-m long initially inclined at an angle of 28.5 degrees to the vertical. If he pushes off with a speed of 2.85 m/s, what is his speed (in m/s) at the bottom of the swing?
Problem 6:
Find the height (in m) from which you would have to drop your textbook so that it would have a speed of 14.2 m/s just before it hits the floor?
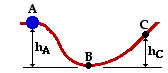Problem 7:
A 0.255-kg bead slides on a curved wire, starting from rest at point A in the diagram at the right. If the wire is frictionless, find the speed of the bead (in m/s) at point C. The height of point A is 5.06 m and the height at point C is 1.91 m.
Problem 8:
A 67.4-kg man jumps from a window 0.783 m above a sidewalk. What is the speed (in m/s) just before his feet strike the pavement?
Problem 9:
Tarzan and Jane, whose total mass is 116-kg, start their swing on a vine 17.7 m long such that the vine is initially at an angle of 30 degrees with the horizontal. At the bottom of the arc, Jane, whose mass is 46.4-kg, steps off. What is the maximum height (in m, relative to the lowest point of the arc) of the tree branch that Tarzan can land on as his swing continues?
Problem 10:
A 0.383-mg flea can jump to a maximum height of about 2.56 cm. Find the speed (in m/s) with which the flea takes off in order to accomplish this amazing feat.
Problem 11:
A spring a has a force constant of 420 N/m. When the spring is stretched 4.84 cm from the equilibrium position, then what amount of energy (in Joules) is stored in the spring?
Problem 12:
A block of mass 0.254 kg is placed on a vertical spring of constant k = 4563 N/m and is pushed downward, compressing the spring a distance of 0.164 m. As the block is released, it leaves the spring and continues to travel upward. Calculate the height (in m) to which the block will rise above the point of release.
Problem Set E
Problem 1:
A child starts from rest at the top of a slide of height 4.57 m. If she reaches the bottom with a speed of 3.91 m/s, what percentage of her total energy at the top of the slide is lost as a result of friction?
Problem 2:
A 77.8-kg diver steps off a 12.44 -meter tower and drops straight down into the water. If he comes to rest 5.14 meters beneath the surface of the water, determine the average resistance force (in Newtons) exerted on the diver by the water.
Problem 3:
A woman weighing 543 N glides across some ice, starting her glide with a speed of 5.46 m/s. If the coefficient of friction between the skates and the ice is 0.164, how far (in m) does she go before coming to rest? Solve this problem by using concepts of work and energy.
Problem 4:
A grocery cart weighing 88.3 N is pushed 6.87 m across the floor by a shopper who exerts a constant horizontal force of 32.8 N. If all frictional forces are neglected, what is the final speed (in m/s) of the cart on the floor surface?
Problem 5:
A 1774-kg car starts from rest at the top of a driveway 6.17 m long which is sloped at an angle of 20.0 degrees with the horizontal. If an average friction force of 3714 N impedes the motion of the car, find the speed (in m/s) of the car at the bottom of the driveway.
Problem 6:
A 38.0-kg child on a swing 2.72 m long is released from rest when the swing supports make an angle of 30.0 degrees with the vertical. If the speed of the child at the lowest position is 2.01 m/s, what is the energy lost due to friction and air resistance (in Joules)?
Problem 7:
In a circus performance, a monkey on a sled is given an initial speed of 4.9 m/s up a 20 degree incline. The combined mass of the monkey and the sled is 28-kg, and the coefficient of kinetic friction between sled and incline is 0.258. How far (in m) will the sled move up the incline?
Problem 8:
A 2.21-kg block is projected up a 30 degrees incline with an initial speed of 6.44 m/s at the bottom. The coefficient of kinetic friction between the block and the incline is 0.744. Find the distance (in m) the block will travel up the incline before coming to rest.
Problem 9:
A woman weighing 542 N glides across some ice, starting her glide with a speed of 4.4 m/s. If the coefficient of friction of between skates and the ice is 0.17, how far (in m) does she go before coming to rest?
Problem 10:
A military plane is designed for vertical takeoff and landing. If the plane has a mass of 8428-kg when fueled, find the work (in Joules) done on the plane by its engines as it accelerates upward at 1.30 m/s/s for a distance of 43.1 m starting from rest.
Problem 11:
A 257-kg crate is pulled parallel to a level surface by an engine. The coefficient of kinetic friction between crate and surface is 0.597. How much power (in W) must the engine deliver to the crate if it has a constant speed of 5.32 m/s?
Problem 12:
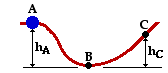The wire in the diagram at the right is frictionless between points A and B and rough between points B and C, and the 0.414-kg bead starts from rest at point A and comes to rest at C, find the total work (in J) done by friction as the bead goes from B to C. The height of point A is 3.57 m and the height of point C is 2.64 m.
Problem 13:
A catcher ' gives' with the ball when he catches a 0.165-kg baseball moving at 38.4 m/s. If he moves his catching glove through a distance of 4.10 cm, what is the average force (in Newtons) acting on his hand?
Problem 14:
If a 79.2-kg man jumps off a 1.16-m high table and lands with his knees and ankles locked, the only cushion for his fall is an approximate 0.585-cm give in the pads of his shoes. Calculate the average force (in Newtons) exerted on him by the ground in this situation. (This average force is sufficient to cause cartilage damage in the joints or to break bones.)
Problem 15:
A 5.40-kg object is lifted vertically through a distance of 6.02 m by a light string under a tension of 82.5 N. Find the final speed (in m/s) of the object if it starts from rest.
Problem 16:
A 69.2-kg athlete runs 643 m at constant speed up a mountain inclined at 20 degrees to the horizontal. He performs this feat in 161 s. Assuming that air resistance is negligible, how much work (in Joules) does he perform?
Problem 17:
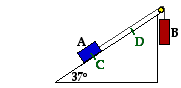Two blocks A and B (with mass 47.1 kg and 171kg, respectively ) are connected by a string as shown in the diagram at the right. The pully is frictionless and of negligible mass. The coefficient of kinetic friction between block A and the incline is 0.271. Determine the change in the kinetic energy (in Joules) of block A as it moves from C to D, a distance of 27.4 m up the incline.
Problem Set F
Problem 1:
A 17.4-kg child on a swing 5.00 meters long is released from rest when the swing supports make an angle of 32.1 degrees with the vertical. Neglecting friction, find the child's speed (in m/s) at the lowest position.
Problem 2:
A 8.69-kg block held at 4.45 meters above the ground slides down a 30 degree, rough incline after being released from rest. Determine the stopping distance (in m) on the rough, horizontal surface if the coefficient of friction is 0.384 for both surfaces.
Problem 3:
A 3.0-kg ball is launched from a cliff at 60 degrees from the horizontal. Determine the maximum height (in meters) that the ball reaches above the valley floor if it has an initial speed of 39.7 m/s. The height of the cliff is 35.4 meters.
Problem 4:
A 13.5-kg box is pushed by from rest by a 223 Newton force directed downward at a 30 degree angle to the horizontal. The coefficient of friction between the box and the floor is 0.448. Determine the box's speed (in m/s) after the box has been moved through a distance of 3.5 meters. HINT: Begin with a free-body diagram.
Problem 5:
A 0.724 kg sphere is compressing a spring (k = 20.2 N/m) a distance of 13.8 cm above its relaxed position When in its relaxed position, the sphere is at a 2.09 m above the floor. If the sphere is released from rest it oscillates up and down as shown in the animation. What is the sphere's speed (in m/s) when it has stretched the spring a distance of 28.9 cm below its relaxed position?
Problem 6:
A 0.55-kg block is shot from a spring-loaded gun. It travels 0.895 meters across a rough table whose coefficient of friction is .326. The force constant of the spring in the gun is 80 N/m and the table top is 0.797 meters above the floor. The spring is compressed a distance of 0.28 meters before the block is released. The block slides off the table and lands on the floor. Determine the speed (in m/s) of the block just before it hits the floor.