Skip to Content Skip to Header Navigation

Stepping Up to PE and KE - Questions 2 Help

Getting your Trinity Audio player ready...

Hold down the T key for 3 seconds to activate the audio accessibility mode, at which point you can click the K key to pause and resume audio. Useful for the Check Your Understanding and See Answers.

The gravitational potential energy (PE) is dependent upon the height of the object. They are directly proportional such that a doubling of the height will double the PE and a halving of the height will halve the PE.

Under certain circumstances, objects will conserve their total amount of mechanical energy over the course of their motion. The sum of their potential energy and kinetic energy will remain constant. As the object falls, there is a transformation of potential energy into kinetic energy (and back) while the total amount of these two forms remains the same.

There are multiple versions of this question that vary from one another in terms of their numerical values. Here is one of the countless number of possible questions.
 

Version 1:

Consider the 4-step staircase. All steps provide an equal elevation gain. The potential energy (PE) on the top step is 44.0 J. Determine the PE and KE values of the ball at the indicated positions.

 


 
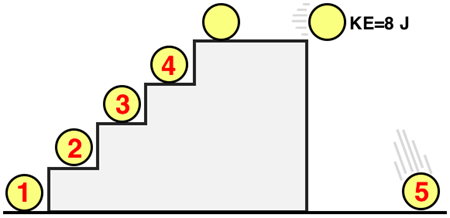
PE1(J): __________
PE2(J): __________
PE3(J): __________
PE4(J): __________
PE5(J): __________
KE5(J): __________


Help for Master Difficulty Level

The Apprentice Difficulty Level involves an energy analysis centered around a staircase with 4 steps. There are two big ideas you need to grasp to successfully complete this Difficulty Level.

Potential Energy
The potential energy (sometimes called the gravitational potential energy and symbolized by PE) is the energy an object possesses due to its vertical position or height. Its value is directly proportional to the height. An object with one-third the height will have one-third the PE.


Mechanical Energy Conservation
The Mechanical Energy is the sum of the potential energy (PE) and kinetic energy (KE). You can assume that mechanical energy is conserved during the falling motion off the back end of the staircase. To say that this energy is conserved is to say that the total amount of it (KE + PE) is not undergoing change. It is the same at each location along the path. So if you know the value for the total mechanical energy (TME) of the ball as it rolls off the top of the staircase, then you know its value at every location, including just prior to the ball striking the ground. The significance of this idea is that the value of KE and PE on the top of the stairs can be used to calculate the value of KE at the bottom of the stairs.

Try this link to The Physics Classroom Tutorial for conducting an energy analysis:

Gravitational Potential Energy

Analysis of Situations in Which Mechanical Energy is Conserved