Force and Energy
If we ignore damping effects, we can conclude that there are two forces acting upon a pendulum - the force of gravity and the tension in the string. The tension force acts perpendicular to the direction the pendulum bob is moving. As such, tension does not do work upon the pendulum bob. At most locations along the circular arc, the force of gravity acts at a non-perpendicular angle to the direction of motion. As such, gravity does work upon a pendulum. Because the force of gravity is a conservative force, it acts to change the potential energy into kinetic energy (and vice versa) without changing the total amount of mechanical energy. So if we ignore the effects of friction and air resistance, we can conclude the total mechanical energy (TME) is conserved.
Potential Energy
The gravitational potential energy (PE) is the energy stored in the pendulum bob due to its vertical position (a.k.a., height). The amount of potential energy possessed by the pendulum bob is directly proportional to the bob's height. So the higher the bob is, the more potential energy that it possesses. And the lower that the bob is, the less potential energy that it will possess. So if a bob is moving downwards, its potential energy is decreasing. And if a bob is moving upwards, its potential energy is increasing.
Kinetic Energy
The total mechanical energy is the sum of the kinetic energy and the potential energy. As discussed in the Force and Energy section, the total amount of mechanical energy is conserved. So the sum of KE and PE should be a constant value. It reasons then that as the potential energy decreases, the kinetic energy will increase. And as the potential energy increases, the kinetic energy will decrease. By putting this information together with the information in the Potential Energy section, you should be able to determine how the kinetic energy is changing as the pendulum bob moves along its circular arc.
Advice About Bar Charts
The bar charts in this question represent the amount of kinetic energy and potential energy possessed by the pendulum bob. The height of each bar is representative of the amount of that type of energy. A location where the pendulum possesses a lot of kinetic energy will be described by a taller KE bar. A location where the pendulum bob possesses no kinetic energy will be described by a smaller (zero) KE bar. The same can be said for potential energy.
Our first piece of advice about bar charts is make sure you understand the content in the previous three sections on this page. There is no short cut to understanding a bar chart that avoids these three sections.
Our next advice is to take your time and analyze each of the three locations on the pendulum path. Ask:
- Which location has the greatest PE?
- Which location has the smallest PE?
- Which location has the greatest KE?
- Which location has the smallest KE?
You will use information from the Potential Energy and the Kinetic Energy sections above to answer these questions. Once you've answered these questions, you can use the heights of the PE and KE bars to match each individual bar chart with a location.
Our final piece of advice is to check your answers before you tap on the Check Answers button. Does everything make sense? If it does, then tap that Check Answers button.
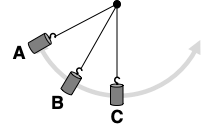 A pendulum is swinging back and forth along its circular arc. Consider locations A, B and C as shown. Match each location to the corresponding energy bar chart.
A pendulum is swinging back and forth along its circular arc. Consider locations A, B and C as shown. Match each location to the corresponding energy bar chart.