The space surrounding a charged object (source charge) is described as having an electric field. The electric field exerts an electrical influence on other objects that enter that space. The electric field value (E) provides a measure of how strong that influence is. The E value at any given location is dependent upon two factors - the quantity of charge (Q) on the source charge and the distance (R) that the location is from the center of the source charge.
 

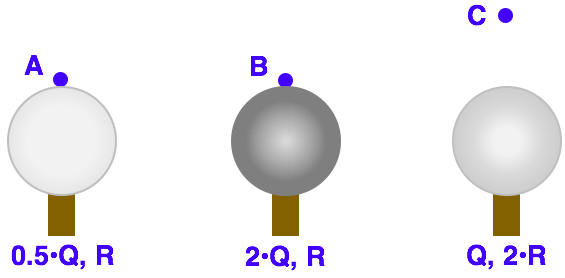
Some problems in Physics don't involve plug-and-chug. They involve the use of an equation as a guide to thinking about how a change in one variable (or two variables) would affect other quantities. That's the case in this question.  Two variables are being changed - the separation distance (R) from a location to the source of charge (i.e., the Van de Graaff generator) and the quantity of charge (Q) on the source. You need to consider both variables and their affect upon the electric field value (E). There's at least two methods of approach. Both rely upon an understanding of the equation (i.e., relationship). 


The Equation
The relationship between the Electric Field value (E), the separation distance (R) and the quantity of charge (Q) is given by the equation ...

E = k•Q/R²

where k is a proportionality constant. From the equation, you would reason that E is directly proportional to the Q. A larger Q results in a larger E value.  And twice the Q would result in twice the E value.

The separation distance (R) works differently. The electric field value (E) is inversely proportional to the square of the separation distance (R). So a larger R value results in a smaller E value. And 2 times the R would result in one-fourth the E value. (The one-fourth is the result of inversing and squaring the 2.) The squaring of the R in the equation means that a change in R will cause a bigger change in E compared to a change in Q.
 

The Application - Method 1
So when you look at the three locations provided, you will note that the location with the largest Q also has the smallest R (or at least a tie for the smallest R). Both a large Q and a small R lead to a large E. And so the Greatest E ranking goes to this location.

The other two locations have different separation distance and a different quantity of charge. In fact in comparing these two locations, one of them has 2 times the charge and 2 times the distance. Two times the charge makes for a larger E but 2 times the distance makes for a smaller E. So you must remember that the effect of the distance is more impactful than the effect of the quantity of charge. So for the two remaining locations, the Smallest E ranking would go to the location that has 2 times the distance..


The Application - Method 2
Another way to approach this task of ranking the three locations involves calculating three different Q/R² ratios. So for each of the three locations, take the charge amount (2Q or 3Q) and divide by the square of the distances (R or 2R). Use a sheet of scratch paper and write down the three ratios. (Paper remembers ratios better than a brain does.) In the case of 2R, be sure to square the 2. When you are done, inspect the coefficients in front of the result. The ratio with the larger coefficient is the one that gets the Greatest E ranking and the ratio with the smallest coefficient gets the Smallest E ranking.