During a collision, an object experiences an impulse that changes its momentum. The impulse is equal to the momentum change. Knowing that impulse is the product of Force•∆Time and that momentum change is the product of Mass•∆Velocity, one can use the Force•∆Time = Mass•∆Velocity relationship as a guide to thinking about how alterations in m, ∆t, and ∆v affect the force in a collision.
Hold down the T key for 3 seconds to activate the audio accessibility mode, at which point you can click the K key to pause and resume audio. Useful for the Check Your Understanding and See Answers.
Case Studies: Impulse and Force - help7
There are two very similar versions of this question. This is one of the two versions:
Version 1
Compare the collision of a gymnast with the floor using two different landing strategies.
Case A: A gymnast strikes the floor with a speed of 12 m/s with relatively stiff-knees as she comes to a stop.
Case B: The same gymnast strikes the floor with a speed of 12 m/s with relaxed knees and some bending as she comes to a stop.
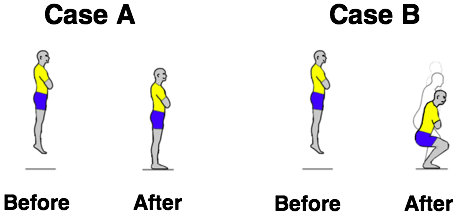
Which variable is different for these two cases?
Which case involves the greatest momentum change? … the greatest impulse? … the greatest force?
Try the links below to our Tutorial for more information:
Momentum and Impulse Connections