The Underlying Principle
Momentum is conserved if the total momentum of the system of two carts is the same Before Collision as it is After Collision. Before the collision, only one of the carts is moving. The stationary cart does not have momentum so the total system momentum is simply the momentum of the moving cart. It's momentum can be calculated from the mass and velocity information. The after collision momentum of the two carts (combined) should be equal to this before collision momentum. Both objects move with the same velocity. The mass and velocity information can be used to determine this after collision momentum. Once determined, you can evaluate whether or not the system momentum is conserved for the situation.
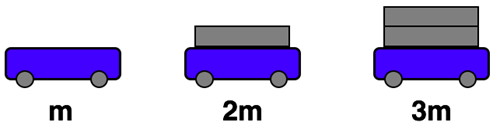
Interpretting the Diagram
The diagrams show a cart that may or may not be loaded with bricks. Each brick has the same mass as a cart. And so a cart with a brick on it has twice the mass as an unloaded cart. And a cart loaded with two bricks has three times the mass as an unloaded cart.
The diagrams also show velocity vectors for the two carts in the After Explosion diagram. The length of the arrow is proportional to the velocity. The arrow lengths are either 1-unit long, 2-units long, 3-units long, 4-units long, or 5-units long.

Calculating the Momentum of a Cart
Momentum is the product of mass and velocity. It might be helpful to call the cart a 1-kg cart. As such, a cart loaded with a brick has a mass of 2 kg and a cart loaded with two bricks has a mass of 3 kg. Such designations would allow you to work with simple numbers that are true to the situation. Similarly, the velocities are 1-unit, 2-units, 3-units, 4-units, or 5-units. So it might also be helpful to refer to these as 1 m/s, 2 m/s, 3 m/s, 4 m/s, and 5 m/s. Doing so allows you to work with numbers and perform quick and simple calculations of momentum from the product of mass and velocity.
Calculating Total System Momentum
Once you have calculated the momentum of the red and blue carts (see above section), it's time to see if the total momentum of the system is the same before the collision as after the collision. Simply add up the momentum of the two carts after the collision and see if it is equal to the momentum of the moving cart before the collision.