The volume of a sample of gas is dependent upon the Kelvin temperature of the gas. Increasing the Kelvin temperature increases the volume. The two quantities are directly proportional to one another. The ratio of Volume/Temperature remains constant. As such, a doubling of the Kelvin temperature will double the volume of the gas.

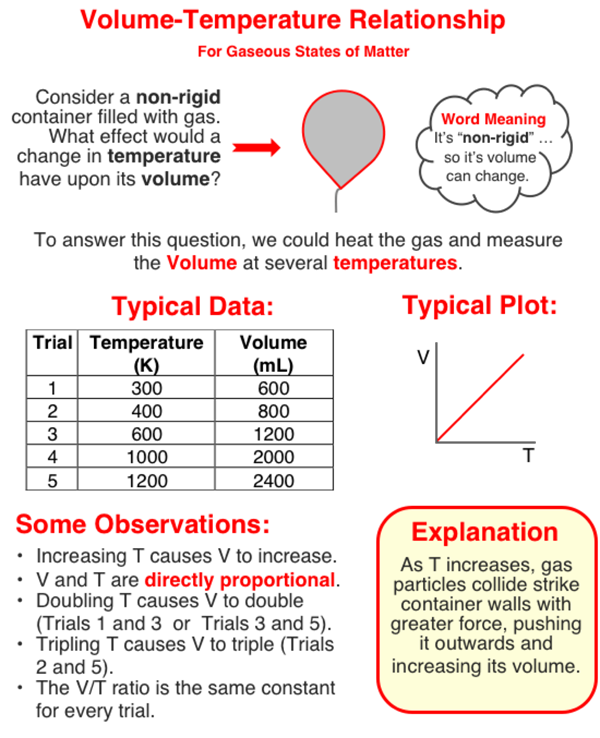
In this question, you need to analyze a set of data to determine the volume when the temperature is 1000 K. One way to do that is to use proportional reasoning. We'll explain that in a moment. But first, take some time to study (and/or scan) the graphic in order to gain familiarity with the volume-temperature relationship. Then continue to the text that continues below the graphic.

Reasoning Proportionally with Volume and Temperature

The temperature of 1000K is two times the temperature of 500 K. And since a doubling of the Kelvin temperature leads to a doubling of the volume, we should be able to use this two times factor to find the answer. Trial 2 of the table has a temperature of 500 K. So the volume at 1000 K will be two times the volume of Trial 2. So your answer can quickly be found by doubling the volume at 500 K.