The pressure of a sample of gas is dependent upon the Kelvin temperature of the gas. Increasing the Kelvin temperature increases the pressure. The two quantities are directly proportional to one another. The ratio of Pressure/Temperature remains constant. As such, a quadrupling of the Kelvin temperature will quadruple the pressure of the gas.

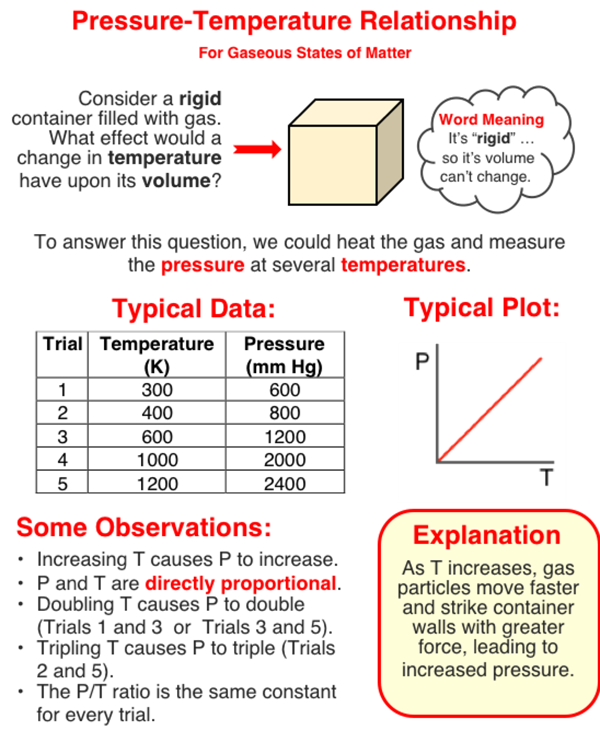
In this question, you need to analyze a set of data to determine the pressure when the temperature is 2000 K. One way to do that is to use proportional reasoning. We'll explain that in a moment. But first, take some time to study (and/or scan) the graphic in order to gain familiarity with the pressure-temperature relationship. Then continue to the text that continues below the graphic.

Reasoning Proportionally with Pressure and Temperature

The temperature of 2000 K is four times the temperature of 500 K. And since four times the Kelvin temperature leads to four times the pressure, we should be able to use this four times factor to find the answer. Trial 2 of the table has a temperature of 500 K. So the pressure at 2000 K will be four times the pressure of Trial 2. So your answer can quickly be found by multiplying the pressure at 500 K by four.