Lesson 2: Relating Stoichiometric Quantities

Part c: Mass-to-Mass Relationships

Part a: Mole-to-Mole Relationships
Part b: Mole-to-Mass Relationships
Part c: Mass-to-Mass Relationships
Part d: Percent Yield
Part e: Stoichiometry Plus

 

The Stoichiometry Problem

Lesson 2 of this Stoichiometry Chapter is loaded with a collection of stoichiometry problems – advice, direction, examples, more examples, and opportunities to practice. These problems provide a balanced chemical equation and an amount of a reactant or product. The unknown quantity to solve for is how much reactant or product would react or be formed. Our solutions demonstrate how to use the factor label method (conversion factors) with an understanding of mole ratios and molar mass to solve for the unknown.
 
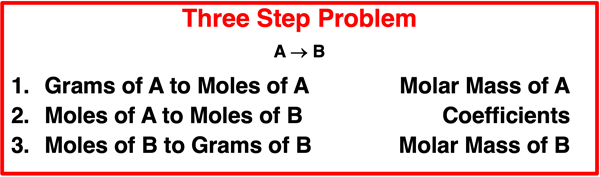
The problems on this page are three-step problems. While this is more steps than previous problems in Lesson 2, the type of problem we will solve is more predictable and routine compared to the two-step problem discussed previously. The basic problem looks like this:

 
We have highlighted in red the given quantity and the desired quantity. Note that the given quantity is the amount of one substance in grams. The desired quantity is the amount of another substance in grams.
 
As we will soon see, the solution first requires the use of a molar mass value for a gram-to-mole conversion of the given substance. Then the coefficients of the balanced chemical equation are used to perform a mole-to-mole conversion. Finally, a molar mass value is used for a gram-to-mole conversion of the desired substance. You will need to use a periodic table to calculate molar mass values for both substances involved in the problem. (If need be, review:  How to Calculate the Molar Mass.)

 

 
 

 

Developing a Plan

Lesson 1 of Chapter 9 was devoted to understanding relationships between quantities. Coefficients in the balanced chemical equation provide the information that relates the moles of one substance to the moles of another substance. Molar mass values provide the information that relates the mass of one substance to the moles of the same substance (or vice versa).  When put together, molar mass values and coefficients allow a student to convert from grams of substance A to grams of substance B.

 
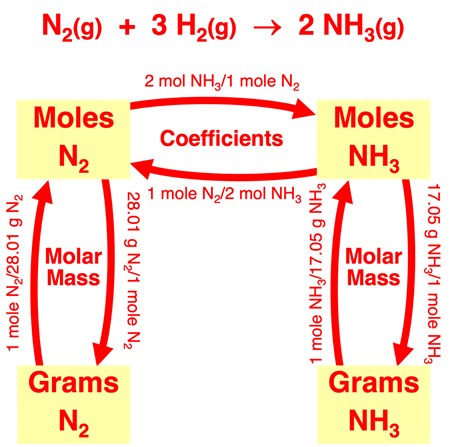
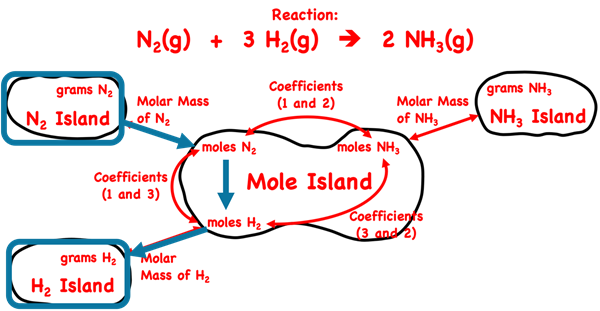
We introduced Mole Island in Lesson 1c. Mole Island is a graphic organizer that helps a student develop a plan for navigating their way through a problem. Mole Island shows what is related to what and how it is related. The graphic below is a version of Mole Island that has been customized for the ammonia synthesis reaction. The mass (in grams) and the moles of each reactant and product are identified on the diagram. Arrows connect these quantities. Each arrow represents a conversion step. One conversion factor is required per arrow. The words next to the arrows (Molar Mass, Coefficients) indicate the information that will be used in the conversion factor.

 
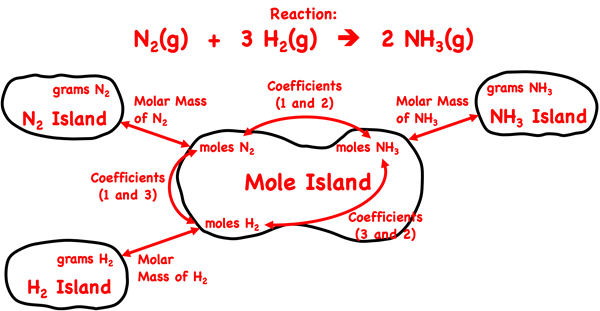
A gram-to-gram conversion, like the problems discussed on this page, requires three steps. There are three arrows separating the grams of one substance and the grams of any other substance. In every case, the first arrow requires a molar mass. The second arrow requires coefficients, and the third arrow requires a second molar mass value. The fact that every gram-to-gram conversion occurs in the same three steps makes these types of problems very predictable.

In the examples that follow, we will discuss the plan for solving the problem, the set-up of conversion factors with units, the insertion of numbers into the conversion factors, and the use of the calculator to solve for the desired quantity.
 
<Sermon>This order is extremely important. Our observation is that the most frequent student frustrations with stoichiometry occur when the early steps are skipped and students rush to their calculator without planning and setting up the solution. The calculator part should be easy. If you are finding it difficult, then you’re probably skipping the first two or three steps of P-U-N-C.</Sermon>
 

 

 

 

Example 1:

Let’s develop a plan and solve the first problem:

 
We have been using Mole Island throughout Lesson 2. We will continue with Mole Island (below) for our planning of a solution. We identify the given quantity – grams of N₂. And we identify the desired quantity – grams of NH₃. We mark both of these on the diagram.

 
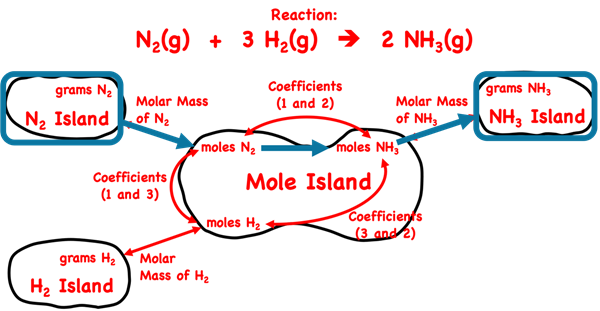
There are three arrows between the given quantity and the desired quantity. From beginning to end, the arrows are labeled as Molar Mass of N₂, Coefficients, and Molar Mass of NH₃. These three arrows describe the three conversions factors in this three-step problem. They are set up below in this very order without any numbers. Observe the unit cancellation. A denominator unit will cancel an identical unit in the numerator of another conversion factor or the unit on the given quantity. We have used pairs of colored diagonal lines to indicate the cancellation of identical units.

 
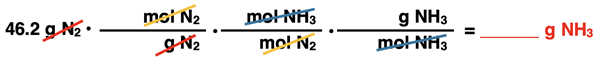
Now it’s time to insert numbers into the conversion factors. Two of the conversion factors are molar mass values. Using a periodic table, we can calculate the molar mass of N₂ and of NH₃. (Review Calculating Molar Mass Values if necessary.)

 
Interpreting these values as 28.01 g N₂/1 mol N₂ and as 17.03 g NH₃/1 mol NH₃ will assist in determining where the numbers are inserted into the conversions factors. For any molar mass conversion factor, the 1 always goes with moles. The 28.01 goes with g N₂ and the 17.03 goes with g NH₃. The middle conversion factor is a mole ratio; the numbers are the coefficients in the balanced chemical equation. The coefficient for N₂ is understood to be a 1 since it is not displayed. Put a 1 next to mol N₂ in the middle conversion factor. The coefficient for NH₃ is 2 so a 2 is placed next to mol NH₃ in the middle conversion factor.

 
Last and definitely least important is the calculation. (“Least important” because it simply follows from the work that has already been done. And if the preliminary work has been done, this last step is very straightforward.) As always, start with the numerical value of the given quantity (46.2) and multiply by all the numbers of the numerators (x1 and x2 and x17.03) and divide by all the numbers of the denominators (÷28.01 and ÷1 and ÷1). The resulting answer is rounded to the proper number of significant digits.
 

 

 

 

Example 2

Now let’s consider the second problem:

 
We begin by using Mole Island to get a plan. We identify the given quantity – grams of N₂. And we identify the desired quantity – grams of H₂. We mark both of these on the diagram.

 
There are three arrows between the given and desired quantity, labeled as Molar Mass of N₂, Coefficients, and Molar Mass of H₂. These three arrows describe the three conversions factors. They are set up below in this very order without any numbers. We have once again used pairs of colored diagonal lines to indicate the cancellation of identical units. (If the conversion factor method is new to you, we recommend our Factor Label Method tutorial page.)

 
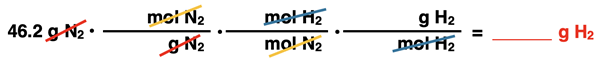
The first conversion factor and the second conversion factor require molar mass values. The molar mass of N₂ was calculated above as 28.01 g N₂/1 mol N₂. The molar mass of H₂ can be calculated from values on the periodic table. The molar mass value is 2.016 g H₂/1 mol H₂. In both conversion factors, the 1 goes with the mol and the molar mass values go with the grams. For coefficients from the balanced chemical equation are used for the middle conversion factor. A 3 goes with mol H₂ and a 1 goes with mol N₂ since these are their coefficients. The inserted numbers are …

 
The last step is to do the calculation. Start with the numerical value of the given quantity (46.2) and multiply by all the numbers of the numerators (x1 and x3 and x2.016) and divide by all the numbers in the denominators (÷28.01 and ÷1 and ÷1). The resulting answer is rounded to the proper number of significant digits.
 
 
 

Example 3

As our final example problem, consider:

 
We begin by identifying and marking the given quantity – grams of NH₃ and the desired quantity – grams of H₂ on Mole Island (below).

 
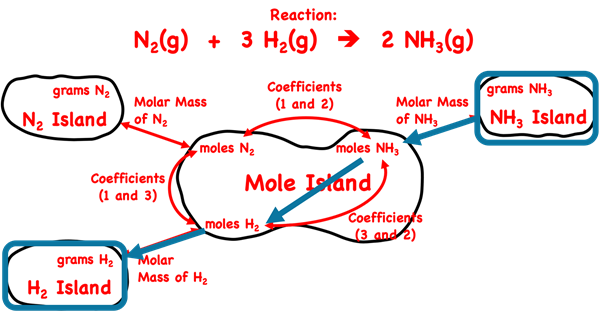
The three arrows, in order, require the use of the Molar Mass of NH₃, Coefficients, and Molar Mass of H₂. These will be the three conversions factors. They are set up below in this very order without any numbers. Pairs of colored diagonal lines are used to indicate the cancellation of identical units. (If the conversion factor method is new to you, we recommend our Factor Label Method tutorial page.)

 
We now insert molar mass values into the first and the third conversion factors. These values have been calculated earlier on this page. They are 17.03 g NH₃/1 mol NH₃ and 2.016 g H₂/1 mol H₂. In these conversion factors, the 1 goes with the moles and the molar mass values go with the grams. The middle conversion factor includes the coefficients for H₂ and NH₃ from the balanced chemical equation. The coefficient in front of H₂ is a 3 and the coefficient in front of NH₃ is a 2.

 
Finish up the last step on your calculator. Start with the numerical value of the given quantity (100.0) and multiply by all the numbers of the numerators (x1 and x3 and x2.016) and divide by all the numbers in the denominators (÷17.03 and ÷2 and ÷1). Round the resulting answer to the proper number of significant digits.
 
 
 
 
 

Before You Leave

• Download our Study Card on Gram-to-Gram Conversions. Save it to a safe location and use it as a review tool. (Coming Soon.)
• Our Stoichiometry Law Breakers Concept Builder provides exceptional practice on the use of the factor label method for solving stoichiometry problems. You will gain a sharp eye for catching mistakes and for internalizing the process of setting up conversion factors to cancel units.
• Practice is incredibly important. The Calculator Pad includes a collection of problems that cover a myriad of Chemistry concepts. Students can check their answers, receive feedback, and have opportunities to correct their answers. It’s a great place to practice. We have five problem sets on Mass-to-Mass Stoichiometry. Problem Sets ST6 through ST10 will be helpful practice.
• Having troubles using Conversion Factors. Study our Factor Label Method page. It discusses the method of using conversion factors to cancel units and solve for an unknown.
• The Check Your Understanding section below include questions with answers and explanations. It provides a great chance to self-assess your understanding.

 
 
 

Check Your Understanding

Use the following questions to assess your understanding. Tap the Check Answer buttons when ready.
 
1. Given:  3 Ti(s)  +  2 N₂(g)  →  Ti₃N₄(s)
The following sets of conversion factors are being used to convert from the given quantity to the desired quantity. Identify any which are incorrectly set up and discuss what is incorrect about it.
 
Given Quantity: 4.56 g Ti₃N₄
Desired Quantity: grams of N₂
 

 

 
 
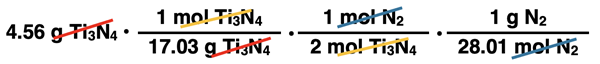
Given Quantity: 287 grams Ti₃N₄
Desired Quantity: grams Ti


 


 
 
Given Quantity: 52.5 g N₂
Desired Quantity: grams of Ti₃N₄
 

 



 
 
2. The following problems pertain to the reaction: 3 Ti(s)  +  2 N₂(g)  →  Ti₃N₄(s).
The problems resemble those discussed in Lessons 2a, 2b, and 2c. For each problem, use Mole Island to determine the number of conversion factors required.

1. Determine the mole of Ti₃N₄ formed from the reaction of 14.5 g Ti. 
   
   Check Answer
   Answer: 2
   
   A molar mass and coefficients
   
    
   
    
2. Determine the mass of N₂ that reacts with 21.5 g of Ti. 
   
   Check Answer
   Answer: 3
   
   Molar mass, coefficients, and molar mass
   
    
   
    
3. Determine the mole of Ti₃N₄ produced when 1.25 moles of N₂ react. 
   
   Check Answer
   Answer: 1
   
   Coefficients only (mole ratio)
   
    
   
    
4. Determine the mass of Ti that must react to produce 35.0 g of Ti₃N₄. 
   
   Check Answer
   Answer: 3
   
   Molar mass, coefficients, and molar mass.
   
    
   
    
5. Determine the moles of N₂ that react to produce 2.48 g of Ti₃N₄. 
   
   Check Answer
   Answer: 2
   
   Coefficients and then molar mass.
   
    
   
    

 
 
3. Show conversion factors and the answer to the following problem.
 
Given:  C₃H₈(g)   +   5 O₂(g)   →   3 CO₂(g)   +   4 H₂O(g)
Determine the grams of CO₂ produced by the combustion of 425 g of C₃H₈.
 

 
4. Show conversion factors and the answer to the following problem.
 
Given:  4 Ti(s)  +  3 O₂(g)  →  2 Ti₂O₃(s)
Determine the grams of Ti₂O₃ produced by the reaction of 99.5 g of Ti.