Lesson 1: Physics in the Early 20th Century
Part d: Wave-Particle Duality
Part 1a: Emission Spectrum of the Elements
Part 1b: The Photon
Part 1c: Bohr's Quantized Energy Levels
Part 1d: Wave-Particle Duality
The Dual Nature of Light
This is not the first time the question has been asked: Is light a particle or a wave? The two conceptions of light seem mutually exclusive. Waves and particles are so different than one another. Waves spread over space. They do not have mass or volume. They are continuous. On the other hand, particles have mass and volume and are located at a specific location. They are quantum. How could any thing be both a particle and a wave?
Prior to the early 1900s, it was a rather accepted idea that light was a wave. A variety of behaviors were observed of light – interference, diffraction, polarization, etc. – that could only be explained if light were a wave. But light as a particle made a strong comeback when Albert Einstein adopted a particle model to explain the photoelectric effect. This effect could not be explained by a wave model.
After Einstein’s success in explaining the photoelectric effect by a particle model, a new answer to the question Is light a particle or a wave? soon emerged. The answer was YES! Light is a particle and light is a wave. It’s just not both at the same time or under the same conditions. It depends on how you look at it. When you look at light undergoing behaviors such as interference and diffraction, you are seeing light’s wavelike nature being displayed. But when you look at light acting as a photon striking the surface of a metal to eject an electron, you are seeing light’s particle-like nature being displayed. The new conception of light as both a particle and a wave was referred to as the dual nature of light.
Image Source: https://commons.wikimedia.org/wiki/File:Wave-particle.jpg
Can Particles Behave as Waves?
In 1924, French physicist Louis de Broglie asked the question:
If light, long thought of as a wave, can exhibit a particle-like nature is it possible that an electron, long thought of as a particle, could exhibit a wave-like nature?
In effect, de Broglie’s hypothesis was that
wave-particle duality was an inherent property of any object – photons, electrons, neutrons, apples, cats, dogs, and cars.
Of course, a wave is characterized by a wavelength. So, de Broglie derived an equation for calculating the wavelength (
λ) of an object. The so-called
de Broglie wavelength equation is
where h is Planck’s constant (6.626 x 10-34 J•s). Loosely put, momentum is the product of an object’s mass and speed. The equation could be written as
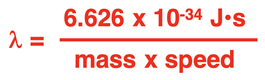
The Wavelength of an Electron
The de Broglie equation can be used to calculate the wavelength of an electron. The electron mass is known to be 9.1 x 10-31 kg. A typical speed of an electron in the Bohr hydrogen atom is 2.2 x 106 m/s. Substituting these values into the de Broglie wavelength equation …
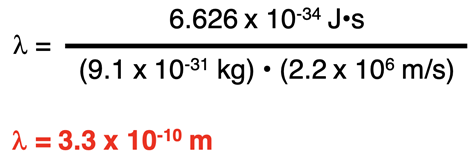
… we can determine an electron with a typical speed to have a wavelength of 3.3 x 10-10 m. This is roughly the circumference of a hydrogen atom according to the Bohr model.
The Wavelength of Everyday Particles
If it is the first time you’ve heard it, then the de Broglie hypothesis that all objects have a dual wave-particle nature should evoke a “Come on. Get serious!” response. The assertion is that an apple, a person, a car, etc. have a wave-like nature … and a wavelength! So, let’s use the de Broglie wavelength equation to determine the wavelength of such particles. The results are shown in the table below.
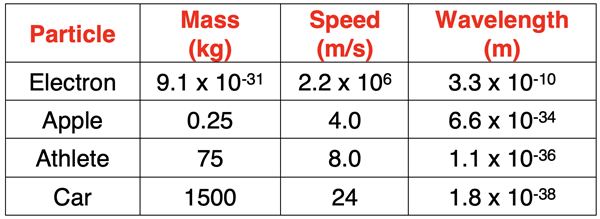
As can be seen in the table, the wavelength of these every day particles is significantly smaller than the wavelength of a typical electron. In fact, the wavelengths are too small to even be observable. Because Planck’s constant is such a small numerical value, the wave-particle duality is only observed of very small particles the size of subatomic particles.
Electrons Behaving as Waves
One of the more interesting behaviors of waves is two-point source interference. The behavior can be observed of water waves, light waves, and sound waves. Waves produced by two nearby sources will interact with one another in such a manner as to cancel each other out at some locations and reinforce each other at other locations. A pattern is produced in which the combined intensity of the two waves fluctuates with location as shown in the animation. The behavior of two-point source interference is regarded as a waves-only behavior.
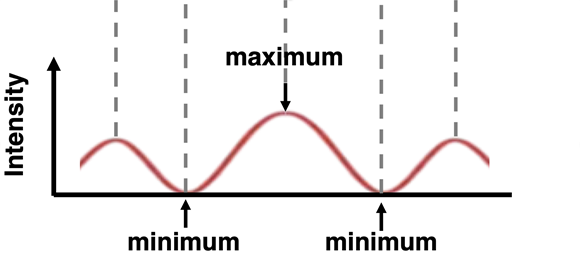
Light can be shown to demonstrate two-point source interference. If a red laser beam is directed towards a slide with a couple of slits on it, the red light will pass through the slits, resulting in two sources of light. The red light from the two sources will subsequently interact with each other to reinforce and cancel out at various locations. When projected onto a screen, the light produces a series of bright bands (from light reinforcement) and dark bands (from light cancellation). The so-called light interference pattern as projected onto the screen is shown below.
Confirming de Broglie’s hypothesis, Clinton Davisson and Lester Germer of Western Electric (later named Bell Labs) were able to show that electrons can exhibit this same behavior as waves. A stream of electrons directed towards a plate with a double slit would produce an interference pattern when projected onto a screen some distance away. Subsequent experiments have shown that electrons exhibit all the behaviors that waves exhibit. Interference and diffraction of electrons is a sign that electrons can get wavy.
Explore More: Ripple Tank Simulation || Interference Patterns Simulation
de Broglie’s Electron Waves
Louis de Broglie’s hypothesis that electrons could exhibit wave-like behaviors motivated him and Niels Bohr to re-think the atom. Bohr modeled the electron as being an orbiting particle. de Broglie suggested that modeling it as a standing wave might be a more accurate approach. Standing waves are commonly observed in ropes and strings. When vibrated at just the right frequency, the rope or string will oscillate in such a way that there are points that appear to be standing still and other points that are vibrating wildly. The standing still locations are known as nodes. The points with lots of back-and-forth movement are known as antinodes. A rope can vibrate with several different standing wave patterns. The patterns differ in terms of the number of nodes and antinodes observed in the pattern. Three such patterns are shown below.
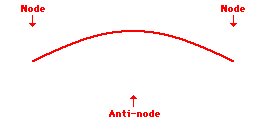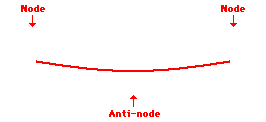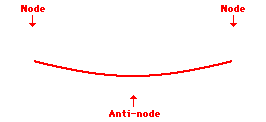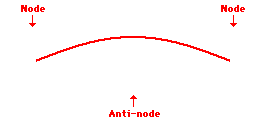
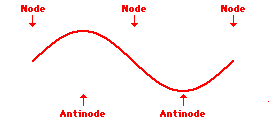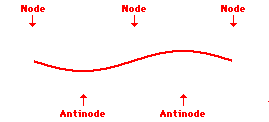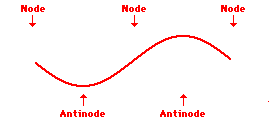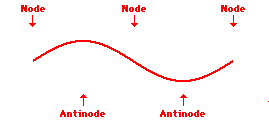
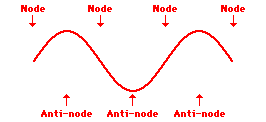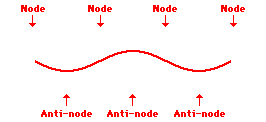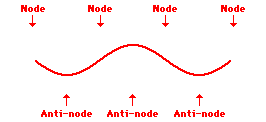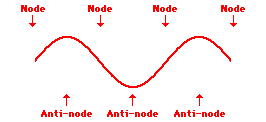
Explore More: Standing Wave Formation Simulation
Louis de Broglie proposed the so-called electron wave model in which the electron was perceived as a standing wave that circled about the nucleus and oscillated inward and outward at the antinodal positions. The number of antinodes and nodes in each electron wave was equal to the principal quantum number. The n=2 orbit was replaced by an electron wave with two antinodes and two nodes. The n=3 orbit was replaced by an electron wave with three antinodes and three nodes. Like Bohr’s orbits, de Broglie’s electron waves were larger for larger quantum numbers.
de Broglie Electron Waves
(n = 2, n = 3, and n = 4)
While the electron wave model never gained widespread acceptance, the idea of treating the electron as a wave did gain acceptance. In fact, the modern model of the atom is sometimes called the wave mechanical model. A wave function is used to describe the electrons within the atom. We will learn more about the wave mechanical model in Lesson 2.
Before You Leave
- The Check Your Understanding section below include questions with answers and explanations. It provides a great chance to self-assess your understanding.
Check Your Understanding
Use the following questions to assess your understanding. Tap the Check Answer buttons when ready.
1. Associate the following statements as being characteristic or attributable to a wave model of light or a particle model of light.
- Has a mass and a volume.
- Described by a wavelength and a frequency.
- Occupies a distinct position.
- Undergoes diffraction.
- Provides a full explanation of the photoelectric effect.
- Is spread about space.
- Undergoes interference.
- Described as being a quantum.
2. Planck’s constant is very small. Suppose that it was one-trillion-billion times bigger (larger by approximately 20 powers of 10). If this were the case, then _____.
- wave-particle duality would no longer exist.
- wave-particle duality would be less noticeable, even among subatomic particles.
- wave-particle duality would be more noticeable; it would be observed for objects that are much larger than subatomic particles.
3. Use the de Broglie wavelength equation to calculate the wavelength of an alpha particle (mass = 6.6 x10
-27 kg) moving with a speed of 1.0 x 10
6 m/s.
4. Explain how the electron wave model is different than the Bohr model of the atom?