What happens when two waves meet while they travel through the same medium? What effect will the meeting of the waves have upon the appearance of the medium? Will the two waves bounce off each other upon meeting (much like two billiard balls would) or will the two waves pass through each other? These questions involving the meeting of two or more waves along the same medium pertain to the topic of wave interference.
What is Interference?
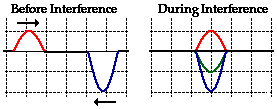
Wave interference is the phenomenon that occurs when two waves meet while traveling along the same medium. The interference of waves causes the medium to take on a shape that results from the net effect of the two individual waves upon the particles of the medium. To begin our exploration of wave interference, consider two pulses of the same amplitude traveling in different directions along the same medium. Let's suppose that each displaced upward 1 unit at its crest and has the shape of a sine wave. As the sine pulses move towards each other, there will eventually be a moment in time when they are completely overlapped. At that moment, the resulting shape of the medium would be an upward displaced sine pulse with an amplitude of 2 units. The diagrams below depict the before and during interference snapshots of the medium for two such pulses. The individual sine pulses are drawn in red and blue and the resulting displacement of the medium is drawn in green.
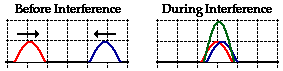
Constructive Interference
This type of interference is sometimes called constructive interference. Constructive interference is a type of interference that occurs at any location along the medium where the two interfering waves have a displacement in the same direction. In this case, both waves have an upward displacement; consequently, the medium has an upward displacement that is greater than the displacement of the two interfering pulses. Constructive interference is observed at any location where the two interfering waves are displaced upward. But it is also observed when both interfering waves are displaced downward. This is shown in the diagram below for two downward displaced pulses.
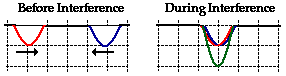
In this case, a sine pulse with a maximum displacement of -1 unit (negative means a downward displacement) interferes with a sine pulse with a maximum displacement of -1 unit. These two pulses are drawn in red and blue. The resulting shape of the medium is a sine pulse with a maximum displacement of -2 units.
Destructive Interference
Destructive interference is a type of interference that occurs at any location along the medium where the two interfering waves have a displacement in the opposite direction. For instance, when a sine pulse with a maximum displacement of +1 unit meets a sine pulse with a maximum displacement of -1 unit, destructive interference occurs. This is depicted in the diagram below.
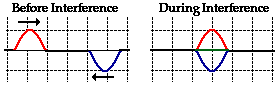
In the diagram above, the interfering pulses have the same maximum displacement but in opposite directions. The result is that the two pulses completely destroy each other when they are completely overlapped. At the instant of complete overlap, there is no resulting displacement of the particles of the medium. This "destruction" is not a permanent condition. In fact, to say that the two waves destroy each other can be partially misleading. When it is said that the two pulses destroy each other, what is meant is that when overlapped, the effect of one of the pulses on the displacement of a given particle of the medium is destroyed or canceled by the effect of the other pulse. Recall from Lesson 1 that waves transport energy through a medium by means of each individual particle pulling upon its nearest neighbor. When two pulses with opposite displacements (i.e., one pulse displaced up and the other down) meet at a given location, the upward pull of one pulse is balanced (canceled or destroyed) by the downward pull of the other pulse. Once the two pulses pass through each other, there is still an upward displaced pulse and a downward displaced pulse heading in the same direction that they were heading before the interference. Destructive interference leads to only a momentary condition in which the medium's displacement is less than the displacement of the largest-amplitude wave.
The two interfering waves do not need to have equal amplitudes in opposite directions for destructive interference to occur. For example, a pulse with a maximum displacement of +1 unit could meet a pulse with a maximum displacement of -2 units. The resulting displacement of the medium during complete overlap is -1 unit.
This is still destructive interference since the two interfering pulses have opposite displacements. In this case, the destructive nature of the interference does not lead to complete cancellation.
Interestingly, the meeting of two waves along a medium does not alter the individual waves or even deviate them from their path. This only becomes an astounding behavior when it is compared to what happens when two billiard balls meet or two football players meet. Billiard balls might crash and bounce off each other and football players might crash and come to a stop. Yet two waves will meet, produce a net resulting shape of the medium, and then continue on doing what they were doing before the interference.
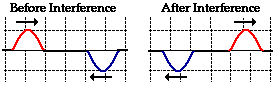
The Principle of Superposition
The task of determining the shape of the resultant demands that the principle of superposition is applied. The principle of superposition is sometimes stated as follows:
|
When two waves interfere, the resulting displacement of the medium at any location is the algebraic sum of the displacements of the individual waves at that same location.
|
In the cases above, the summing the individual displacements for locations of complete overlap was made out to be an easy task - as easy as simple arithmetic:
|
Displacement of Pulse 1
|
Displacement of Pulse 2
|
=
|
Resulting Displacement
|
|
+1
|
+1
|
=
|
+2
|
|
-1
|
-1
|
=
|
-2
|
|
+1
|
-1
|
=
|
0
|
|
+1
|
-2
|
=
|
-1
|
In actuality, the task of determining the complete shape of the entire medium during interference demands that the principle of superposition be applied for every point (or nearly every point) along the medium. As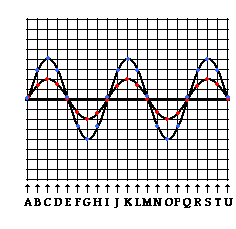 
an example of the complexity of this task, consider the two interfering waves at the right. A snapshot of the shape of each individual wave at a particular instant in time is shown. To determine the precise shape of the medium at this given instant in time, the principle of superposition must be applied to several locations along the medium. A short cut involves measuring the displacement from equilibrium at a few strategic locations. Thus, approximately 20 locations have been picked and labeled as A, B, C, D, etc. The actual displacement of each individual wave can be counted by measuring from the equilibrium position up to the particular wave. At position A, there is no displacement for either individual wave; thus, the resulting displacement of the medium at position will be 0 units. At position B, the smaller wave has a displacement of approximately 1.4 units (indicated by the red dot); the larger wave has a displacement of approximately 2 units (indicated by the blue dot). Thus, the resulting displacement of the medium will be approximately 3.4 units. At position C, the smaller wave has a displacement of approximately 2 units; the larger wave has a displacement of approximately 4 units; thus, the resulting displacement of the medium will be approximately 6 units. At position D, the smaller wave has a displacement of approximately 1.4 units; the larger wave has a displacement of approximately 2 units; thus, the resulting displacement of the medium will be approximately 3.4 units. This process can be repeated for every position. When finished, a dot (done in green below) can be marked on the graph to note the displacement of the medium at each given location. The actual shape of the medium can then be sketched by estimating the position between the various marked points and sketching the wave. This is shown as the green line in the diagram below.
We Would Like to Suggest ...
Why just read about it and when you could be interacting with it? Interact - that's exactly what you do when you use one of The Physics Classroom's Interactives. We would like to suggest that you combine the reading of this page with the use of our
Wave Addition Interactive. You can find it in the Physics Interactives section of our website.
Visit:
Wave Addition Interactive
Check Your Understanding
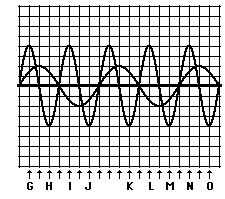1. Several positions along the medium are labeled with a letter. Categorize each labeled position along the medium as being a position where either constructive or destructive interference occurs.
2. Twin water bugs Jimminy and Johnny are both creating a series of circular waves by jiggling their legs in the water. The waves undergo interference and create the pattern represented in the diagram at the right. The thick lines in the diagram represent wave crests and the thin lines represent wave troughs. Several of positions in the water are labeled with a letter. Categorize each labeled position as being a position where either constructive or destructive interference occurs.